La programmation dynamique

Numérique et sciences informatiques

I. Introduction

La programmation dynamique, introduite au début des années 1950 par Richard Bellman, est une méthode permettant de résoudre efficacement certains problèmes en combinant les solutions de sous-problèmes, à l’image des méthodes de type diviser pour régner.
Un algorithme de programmation dynamique repose sur l'idée de décomposer un problème en sous-problèmes plus petits, puis de mémoriser leurs solutions afin d'éviter de recalculer les mêmes résultats plusieurs fois..
Cette technique est particulièrement utile pour les problèmes d’optimisation, tels que ceux rencontrés en algorithmique combinatoire (rendu de monnaie, sac à dos, alignement de séquences, etc.)..

II. Principe de la programmation dynamique

Le principe de la programmation dynamique est est utilisée lorsque des sous-problèmes se répètent. Le pricnipe est le suivant :

  1. Décomposer le problème en sous-problèmes.
  2. Résoudre chaque sous-problème une seule fois.
  3. Stocker les résultats pour éviter les recalculs.
  4. Combiner les solutions pour obtenir le résultat final.

III. Exemple : la suite de Fibonacci

Reprenons l'exemple classique de récursivité multiple qu'est celui de la fonction de Fibonacci définie mathématiquement par :

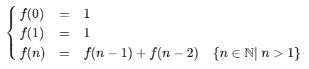
Fibonacci 
def fibonacci(n):
    """
    Calcule la valeur de la suite de Fibonacci pour un entier n.
        Entrée : n (int) : entier positif ou nul
        Sortie : int : valeur de la suite de Fibonacci(n)
    """
    if n < 0:
        raise ValueError("n doit être un entier positif ou nul")
    if n == 0:
        return 0
    if n == 1:
        return 1
    return fibonacci(n - 1) + fibonacci(n - 2)

Dans la version récursive, pour calculer fibonacci(5), on calcule d’abord fibonacci(4) et fibonacci(3). Pour calculer fibonacci(4), on calcule fibonacci(3) et fibonacci(2). Pour calculer fibonacci(3), on calcule fibonacci(2) et fibonacci(1)... Le déroulement du processus est arborescent comme le montre la figure ci-dessous.

Fibonacci
On remarque que les branches de l’arbre se divise en deux à chaque niveau (sauf en bas de l’arbre, ie. à droite sur la figure), ce qui traduit le fait que la fonction fibonacci s’appelle elle-même deux fois à chaque fois qu’elle est invoquée avec n > 1.
On se rend compte qu'il y a beaucoup d'appels redondants : fib(1) a été lancé 5 fois, fib(2) a été lancé 3 fois, etc.
Ces redondances entraînent un nombre d'appels récursifs qui explose rapidement dès que n est élevé. Par conséquent, les temps de calcul deviennent vite très élevés.

Il existe plusieurs solutions pour obtenir un coût plus raisonnable.
Une solution que nous allons adopter consiste à mémoriser le résultat des calculs une fois qu’ils auront été calculés de manière à ne pas refaire deux fois le même calcul. 

def fibo(n):
	F = [0]*(n+1) # Initialisation du tableau
	F[1] = 1 # terme de rang 1
	for i in range(2,n+1) :
		F[i] = F[i-1] + F[i-2]
	return F[n]
Remarque : Cette solution n'est pas récursive avec une complexité en O(n).

La fonction fibo(n) prend en entrée un entier n et retourne le n-ème nombre de Fibonacci. La fonction utilise une méthode itérative basée sur la programmation dynamique pour calculer ce nombre.

Les deux premiers nombres de Fibonacci sont définis manuellement (0 et 1). Ensuite, on itère sur les entiers de 2 à n inclus. Pour chaque entier i, on calcule le nombre de Fibonacci correspondant F[n] en utilisant la formule de récurrence F[n] = F[n-2] + F[n-1], où F[n-2] et F[n-1] sont les deux nombres de Fibonacci précédents.

Cet exemple illustre la méthode itérative basée sur la programmation dynamique qui permet de calculer les nombres de Fibonacci de manière efficace et évite la répétition de calculs inutiles.

III. Exemples de problèmes résolus par la programmation dynamique

  1. Alignement de séquences

    2. Le problème de l'alignement de séquences consiste à trouver la meilleure correspondance entre deux séquences de caractères (par exemple, des séquences d'ADN ou de protéines). La programmation dynamique permet de résoudre ce problème en décomposant le calcul de l'alignement optimal en plusieurs sous-problèmes plus petits. On utilise une table pour stocker les résultats intermédiaires et éviter de les recalculer plusieurs fois.

  2. Rendu de monnaie

    3. Le problème du rendu de monnaie consiste à trouver la façon la plus efficace de rendre une somme d'argent donnée en utilisant un ensemble de pièces de monnaie. La programmation dynamique permet de résoudre ce problème en décomposant le calcul de la solution optimale en plusieurs sous-problèmes plus petits. On utilise une table pour stocker les résultats intermédiaires et éviter de les recalculer plusieurs fois.

V. Conclusion

La programmation dynamique est une technique clé en algorithmique qui permet d’améliorer les performances de nombreux algorithmes de combinatoire et d’optimisation.

Avantages :

  • Accélère les calculs en évitant la redondance des sous-problèmes.
  • Transforme des algorithmes exponentiels en O(n) ou O(n²).

Inconvénients :

  • Peut consommer beaucoup de mémoire (tableaux stockant des sous-solutions).

Savoir faire

  • Utiliser la programmation dynamique pour écrire un algorithme.
  • Découvrir l’intérêt de la programmation dynamique pour les recherches d’alignement de séquences.

Fiche de cours