Algorithmes sur les graphes
Numérique et Sciences Informatiques

Algorithmes sur les graphes : parcours
Le parcours d’un graphe consiste à visiter tous ses sommets de manière systématique. Deux algorithmes classiques permettent d’effectuer ce parcours :
- Le parcours en profondeur (Depth-First Search, DFS), qui explore autant que possible un chemin avant de revenir en arrière.
- Le parcours en largeur (Breadth-First Search, BFS), qui explore d’abord les sommets proches avant de s’éloigner progressivement.
Ces algorithmes maintiennent généralement deux structures :
- Une liste des sommets déjà rencontrés (
déjà_vus), qui évite de revisiter un sommet. - Une liste des sommets en cours de traitement (
à_traiter), qui suit l’ordre dans lequel les sommets doivent être explorés.
Coût du parcours
Soit n = |V| le nombre de sommets et p = |E| le nombre d’arêtes du graphe.
- Chaque sommet est inséré au plus une fois dans la liste
à_traiter, puis retiré une fois. Si cette liste est implémentée avec une pile (DFS) ou une file (BFS), les opérations d’insertion et de suppression sont en temps constant. Ainsi, la gestion de cette structure est en O(n). - Chaque liste d’adjacence est parcourue au plus une fois, ce qui donne un coût de O(p) pour examiner les voisins.
- Si la vérification d’un sommet dans
déjà_vusest en temps constant (ce qui est le cas avec une table de hachage ou un ensemble), alors le coût total du parcours est en O(n + p).
Ce résultat est optimal pour parcourir un graphe représenté par des listes d’adjacence.
Parcours en largeur
L’algorithme de parcours en largeur (Breadth-First Search, BFS) explore un graphe en visitant d’abord tous les sommets situés à une même distance du sommet initial avant de passer aux suivants. Pour cela, il utilise une file d’attente où sont stockés les sommets à traiter.
Principe du BFS
- On démarre depuis un sommet
s, qui est ajouté à la file et marqué comme découvert. - Tant que la file n’est pas vide :
- On en retire le premier sommet.
- On ajoute ses voisins non encore visités à la file, en les marquant comme découverts.
- Les sommets sont donc traités par niveau :
- Tous ceux situés à distance 1 de
ssont explorés avant ceux à distance 2, puis distance 3, etc.
- Tous ceux situés à distance 1 de
Grâce à cette propriété, le BFS est particulièrement utile pour calculer la plus courte distance entre deux sommets dans un graphe non pondéré.
Exemple de parcours en largeur
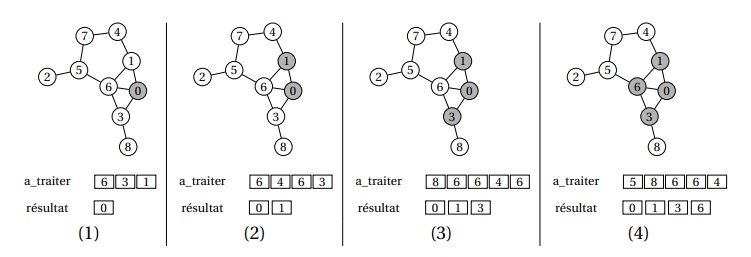
Considérons un graphe G :
- Un parcours en largeur depuis 0 peut donner l'ordre :
0 → 1 → 3 → 6 → 4 → 8 → 5 → 7 → 2. - Un parcours en largeur depuis 2 peut donner l'ordre :
2 → 5 → 6 → 7 → 0 → 1 → 3 → 4 → 8.
1. Fonction PARCOURS_LARGEUR(G, s)
2. Créer une file vide a_traiter
3. Enfiler le sommet s dans a_traiter
4. Créer un ensemble découverts
5. Ajouter s à découverts
6. Tant que a_traiter n'est pas vide :
7. Retirer un sommet u de a_traiter (défiler)
8. Ajouter u à la liste des sommets découverts
9.
10. Pour chaque voisin v de u dans G :
11. Si voisin n'est pas dans découverts :
12. Ajouter voisin à découverts
13. Enfiler voisin dans a_traiter
14.
15. Fin de la fonction
Entraînement 1 :
Implémenter une fonction pour un parcours en largeur d'un graphe G à partir d'un sommet S. G est représenté par une liste d'adjacence.
Voir une solutionParcours en profondeur (DFS)
L’algorithme de parcours en profondeur (Depth First Search, DFS) explore un graphe en suivant un chemin aussi loin que possible avant de revenir en arrière. Pour cela, il utilise une pile où sont stockés les sommets à explorer.
Principe du DFS
- On démarre depuis un sommet
s, qui est ajouté à la pile et marqué comme visité. - Tant que la pile n’est pas vide :
- On dépile le dernier sommet ajouté.
- On explore un de ses voisins non visités.
- Ce voisin est ajouté à la pile et marqué comme visité.
- Si un sommet n’a plus de voisins non visités, on remonte en arrière dans la pile.
- Le DFS explore donc chaque branche du graphe jusqu’au bout avant d’explorer une autre branche.
Cet algorithme est utile pour :
- Détecter la présence de cycles dans un graphe.
- Explorer toutes les connexions d'un graphe ou d’un arbre.
Exemple de parcours en profondeur
Considérons un graphe G :
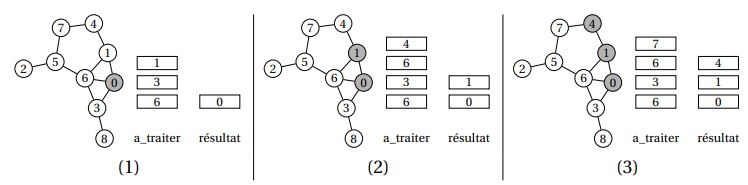
Sur ce graphe :
- Un parcours en profondeur depuis 0 peut donner l'ordre :
0 → 1 → 4 → 7 → 5 → 2 → 6 → 3 → 8. - Un parcours en profondeur depuis 2 peut donner l'ordre :
2 → 5 → 6 → 0 → 1 → 4 → 7 → 3→ 8.
1. Début Fonction PARCOURS_PROFONDEUR(G, s)
2. a_traiter ← pile vide
3. Empiler s dans a_traiter
4. decouverts ← liste vide
5.
6. Tant que a_traiter n'est pas vide faire
7. sommet ← Dépiler a_traiter
8.
9. Si sommet n'est pas dans decouverts alors
10. Ajouter sommet à decouverts
11.
12. Pour chaque voisin v de G[sommet] triés par ordre décroissant faire
13. Si v n'est pas dans decouverts alors
14. Empiler v dans a_traiter
15. Fin Si
16. Fin Pour
17.
18. Fin Si
19.
20. Fin Tant que
21.
22. Retourner decouverts
23. Fin de la fonction
Cette version utilise la récursivité pour explorer directement les voisins du sommet courant.
1. Fonction DFS_REC(G, s, VISITÉS)
2. Ajouter s à VISITÉS
3. Afficher s (ou l'ajouter à la liste des sommets visités)
4.
5. Pour chaque voisin v de s dans G :
6. Si v n'est pas dans VISITÉS :
7. Appeler DFS_REC(G, v, VISITÉS)
8.
9. Fin de la fonction
Entraînement 2 :
Implémente une fonction parcours_profondeur(G, s) qui prend en entrée un graphe G (représenté sous forme de dictionnaire de listes d’adjacence) et un sommet de départ s. La fonction doit afficher l’ordre des sommets visités.
Cycle dans les graphes
Application : Réseau routier
Entraînement :
Un réseau routier est représenté par un graphe pondéré, qui peut être orienté si les trajets sont dans un sens unique ou si les temps de trajet varient en fonction du sens. Dans ce graphe, les villes sont les sommets et les routes sont les arêtes. Les distances ou temps de trajet sont représentés sur les arêtes.
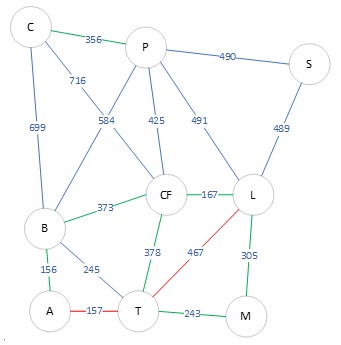
Entraînement 3 :
Écrire une variable Python sommets représentant les villes dans le graphe.
Entraînement 4 :
Représenter le graphe sous forme d'un dictionnaire graph, où chaque clé est une ville et chaque valeur est la liste de ses voisins (les villes connectées par des routes).
Entraînement 5 :
Représenter le graphe sous forme de matrice d’adjacence matrice, où chaque cellule (i, j) représente la distance ou le temps entre les villes i et j. Si deux villes ne sont pas connectées, la cellule contient un infini ou une valeur indicatif.
Entraînement 6 :
Écrire une fonction villes(graph) qui, à partir d’un graphe représenté par un dictionnaire, renvoie la liste des sommets (villes) dans le graphe.
Entraînement 7 :
Écrire une fonction voisins(graph, ville1) qui renvoie la liste des voisins (villes adjacentes) de la ville ville1 dans un graphe non orienté.
Entraînement 8 :
Écrire une fonction sont_voisins(graph, ville1, ville2) qui renvoie True si les villes ville1 et ville2 sont adjacentes dans le graphe, sinon False.
Entraînement 9 :
Écrire une fonction distance(graph, matrice, ville1, ville2) qui renvoie la distance (ou le temps de trajet) entre les villes ville1 et ville2 si elles sont adjacentes, sinon une valeur indiquant qu’il n’y a pas de connexion directe.
Entraînement 10 :
Écrire une fonction chemin(graph, ville1, ville2) qui retourne la liste des villes à parcourir pour aller de ville1 à ville2. L’utilisation d’un parcours en profondeur est recommandée pour cette tâche.
Entraînement 11 :
Écrire une fonction distance_chemin(graph, matrice, ville1, ville2) qui renvoie la distance totale (ou le temps total) du chemin le plus court entre les villes ville1 et ville2, calculée en utilisant la fonction chemin définie précédemment.
Entraînement 12 :
Implémenter l’algorithme de Dijkstra pour déterminer le plus court chemin entre deux villes du réseau routier (en distance ou en temps, au choix).
Savoir faire
- Savoir parcourir un graphe en profondeur et en largeur.
- Savoir repérer la présence d’un cycle dans un graphe
- Savoir chercher un chemin dans un graphe.
Fiche de cours