Les arbres

Numérique et sciences informatiques

donnees

Les arbres :

Les arbres sont maintenant une notion familière pour nous :

  • arbres généalogiques
  • tournois sportifs
  • fichiers de nos ordinateurs
  • sites web
C’est une structure de donnée extrêmement riche de type abstrait, dont nous allons maintenant explorer quelques aspects.

Un arbre est une structure de données :

  • non-linéaire (comparée aux tableaux, listes, piles, et files qui sont des structures linéaires)
  • hiérarchique
  • récursive (un arbre peut être définie récursivement comme un ensemble de noeuds accessibles depuis un noeud racine. Chaque noeud étant une structure composée d’une valeur et d’une liste de références vers d’autres noeuds, avec les contraintes suivantes : aucune référence n’est dupliquée (chaque noeud a un unique parent),et aucune référence ne désigne le noeud racine (qui n’a donc pas de parent).

Définition :

Un arbre est un graphe simple non orienté, acyclique et connexe. (théorie des graphes).

  • Un graphe simple est un graphe dans lequel il n’existe pas d’arête reliant un sommet à lui-même et dans lequel deux sommets distincts sont reliés par au plus une arête ;
  • un graphe acyclique est un graphe dans lequel il n’existe pas de chemin fermé ;
  • un graphe connexe est un graphe dans lequel il existe toujours un chemin reliant deux sommets distincts.

Une conséquence de ces deux dernières propriétés est que pour tout couple de sommets (r,s) il existe un unique chemin qui conduit de r à s, et que le choix de r induit une orientation implicite du graphe. Dans ce cas, on dit que l’arbre est enraciné et que r est la racine de l’arbre.

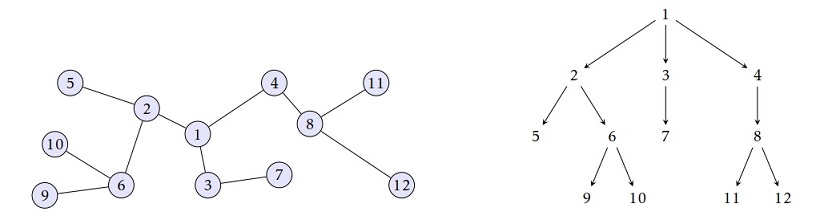
arbres
Un arbre et son enracinement à partir du sommet 1

Dans l’exemple ci-dessus, le sommet 1 est la racine de l’arbre.
Si une arête mène du sommet i au sommet j, on dit que i est le père de j, et en conséquence que j est le fils de i.
Par exemple, le sommet 3 est le père de 7, le sommet 6 est le fils de 2.
Il est d’usage de dessiner un arbre en plaçant un père au dessus de ses fils, si bien que l’on peut sans ambiguïté représenter les arêtes par des traits simples à la place des flèches, ce que l’on fera par la suite.

Quand un graphe est un arbre on parle plus facilement de noeud que de sommet. On distingue les noeuds externes (les feuilles) qui n’ont pas de fils des noeuds internes qui en ont. Dans l’exemple ci-dessus, les feuilles sont les sommets 5, 7, 9, 10, 11, et 12 et les noeuds internes les sommets 1, 2, 3, 4, 6 et 8.

Enfin, on notera que chaque noeud est la racine d’un arbre constitué de lui-même et de l’ensemble de ses descendants ; on parle alors de sous-arbre de l’arbre initial. Par exemple, les sommets 2, 5, 6, 9 et 10 constituent un sous-arbre enraciné en 2 de l’arbre représenté ci-dessus. Il arrivera fréquemment qu’on identifie le noeud et le sous-arbre dont il est la racine. Les arbres sont des structures récursives. Ces arbres sont eux mêmes constitués d'arbres.

La profondeur d'un sommet est la distance à la racine (nombre d’arête qu’il faut parcourir pour atteindre ce noeud à partir de la racine de l'arbre). Dans l'exemple, la profondeur du sommet 6 est 2 (P(6) = 2). ou P(1) = 0 ou P(8) = 2.

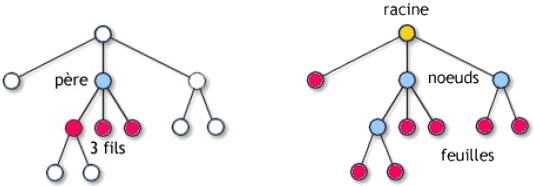
arbres
Schéma d'un arbre T

La hauteur d'un arbre correspond à la distance maximale entre une feuille et la racine. La hauteur de l’arbre dessiné est égale à 3 si la profondeur de la racine est de 0.
Il est également possible de définir la hauteur de l’arbre vide comme étant égale à -1.

On appelle étiquette l’information attachée à un nœud, une feuille ou une arête.

L’arité d’un nœud représente le nombre de ses fils. Ainsi, les feuilles sont des nœuds d’arité 0. Un arbre binaire strict est un arbre où chaque nœud interne a une arité de 2.

Un arbre binaire est une structure finie d'éléments qui peut :

  • être égal à l’ensemble vide (aucun nœud ; arbre vide) ;
  • consister en une feuille f ;
  • consister en une racine n, et deux arbres binaires distincts g et d appelés fils gauche et fils droit — noté (n,\ g,\ d).

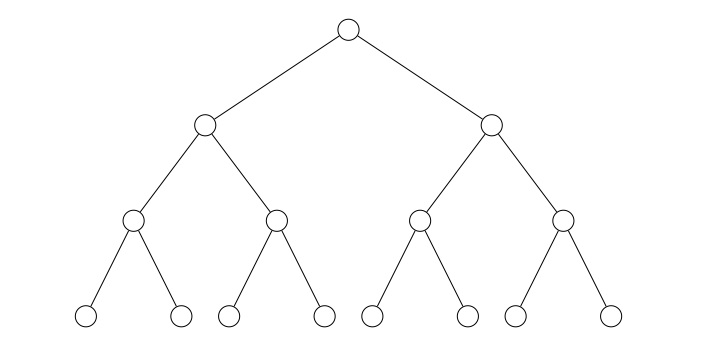
Un arbre binaire est complet si chaque nœud est soit une feuille, soit un nœud ayant 2 enfants. Un arbre binaire parfait est un arbre où toutes les feuilles sont à la même distance de la racine (toutes les feuilles ont la même profondeur).

arbres
Un exemple d'arbre binaire parfait

Entraînement 1 :

Considérons l’arbre T (tree) suivant :

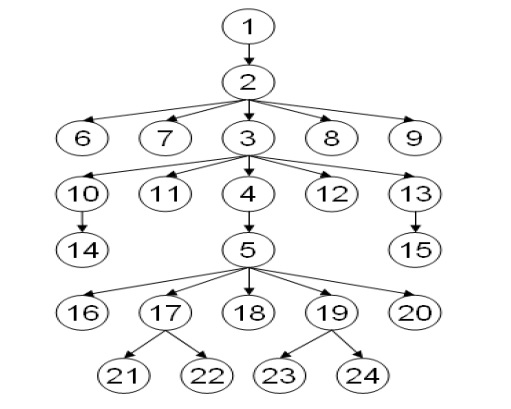
arbres
arbre T

  1. Déterminer pour l’arbre T, sa racine, sa taille, sa hauteur, ses noeuds intérieurs et ses feuilles.
    2. Voir une solution

  2. Pour le noeud 4, déterminer son parent, ses frères, sa profondeur, ses ancêtres et ses descendants propres.
    3. Voir une solution

  3. Pour le noeud 17, déterminer son parent, ses frères, sa profondeur, ses ancêtres et ses descendants propres.
    4. Voir une solution

    Entraînement 2 :

    Soit le tableau suivant qui représente un arbre T en triplets (info, gauche, droit) :

    Indice du noeud 0 1 2 3 4 5 6 7 8 9
    Étiquette du noeud 23 2 3 5 7 11 13 37 41 19
    Indice du fils gauche -1 4 3 -1 -1 9 -1 8 6 -1
    Indice du fils droit -1 5 0 -1 -1 -1 2 1 -1 -1

    La première colonne (indice 0) représente le noeud dont le champ info est 23 (valeur du noeud), le champ gauche est -1 (indice du fils gauche) et le champ droit est -1 (indice du fils droit).
    La seconde colonne (indice 1) représente le noeud dont le champ info est 2, le champ gauche est 4 et le champ droit est 5, et ainsi de suite.
    La valeur (-1) indique l’absence d’un fils gauche ou droit.
    Le noeud d'indice zéro n'est pas la racine de l'arbre.

    1. Représenter cette arbre à partir de sa racine
    2. Donner le nom des sommets qui sont des feuilles
    3. Donner le nom des sommets qui ne sont pas des feuilles
      Aide

    4. Donner la hauteur de l'arbre T
    Voir une solution


On peut créer une classe pour les arbres binaires avec une classe Noeud et une classe ArbreBinaire. 

from graphviz import Digraph

class Noeud():
    """Représente un noeud dans un arbre binaire
    - Propriétés :
        * valeur : valeur du noeud
        * gauche : noeud gauche ou None
        * droit  : noeud droit ou None
    - Méthodes   :
        * est_feuille() 
        * __repr__() : affichage d'un noeud"""
    
    def __repr__(self):
        """la méthode __repr__ définit ce qui sera affiché
        lorsqu'on tapera l'objet dans Jupyter ou un terminal
        Ici, on affiche juste la valeur du noeud"""
        return str(f"## {self.valeur} ##")
    
    def __init__(self,valeur):
        self.valeur = valeur
        self.gauche = None
        self.droit = None

    
class Arbrebin():
    """Représente un objet arbre binaire
    - Propriétés : 
        * racine : objet de type Noeud désignant la racine de l'arbre
    - Méthodes :
        * show() : représentation graphique de l'arbre à l'aide de graphviz
    """
     
    def __init__(self, nd = None):
        # Initialise l'arbre à vide par défaut, sinon avec un noeud passé en paramètre optionnel
        self.racine = nd
    
    def importe(self, tableau):
        """Importe un arbre depuis un tableau
        ["Noeud", [S_A_G], [S_A_D]]
        [ ] désigne un arbre vide"""
        def importe_tableau(tableau):
            # Cas particuliers
            if tableau == []:
                return None
            if len(tableau) == 1:
                return Noeud(tableau[0])

            # tableau a une longueur >= 2
            nd = Noeud(tableau[0])
            nd.gauche = importe_tableau(tableau[1])
            nd.droit  = importe_tableau(tableau[2]) if len(tableau) > 2 else None
            return nd
        
        self.racine = importe_tableau(tableau)
        
	def show(self):
	    """Renvoie un objet graphviz pour la visualisation graphique de l'arbre"""
	    def representation(dot, noeud):
	        # Ajoute la représentation du noeud à la représentation dot de l'arbre
	        if noeud is not None:
	            dot.node(str(id(noeud)), str(noeud.valeur))
	            # Appel récursif de la fonction representation
	            if noeud.gauche is not None:
	                dot.edge(str(id(noeud)), str(id(noeud.gauche)), label='gauche')
	                representation(dot, noeud.gauche)
	            if noeud.droit is not None:
	                dot.edge(str(id(noeud)), str(id(noeud.droit)), label='droit')
	                representation(dot, noeud.droit)

	    dot = Digraph(comment="Arbre binaire", format='svg')
	    dot.attr('node', shape='circle')  # Définit la forme des nœuds
	    dot.attr('edge', arrowhead='vee')  # Définit le style des flèches
	    dot.attr(rankdir='TB')  # Orientation de haut en bas

	    representation(dot, self.racine)
	    return dot

    
    def taille(self):
        """Renvoie la taille de l'arbre"""
        def taille_arbre(nd):
            # condition d'arrêt
            if nd is None:
                return 0
            # Appel récursif
            return 1 + taille_arbre(nd.gauche) + taille_arbre(nd.droit)
        
        return taille_arbre(self.racine)

Pour visualiser l'utilisation des classes Noeud et ArbreBin, nous allons utiliser le module Digraph en ligne afin de vérifier et visualiser les résultats.


Entraînement 4 :

En utilisant la classe Noeud() précédente, on va créer un objet arbre qui aura 3 propriétés (ou attributs) :

  • La propriété valeur contiendra la valeur associée au noeud.
  • Les propriétés gauche et droit seront les sous arbres gauche et droit.

Les deux propriétés gauche et droit seront des instances de la classe Noeud. Si il n'y a pas de sous arbre gauche ou droit, on indiquera la valeur None dans les propriétés correspondantes.

Créer 3 méthodes dans la classe Noeud :

  1. La méthode est_feuille() renverra un booléen selon que l'objet est une feuille ou non.
  2. La méthode cree_fils_gauche() prend en paramètre une valeur et crée une feuille à gauche dont la valeur est passée en paramètres.
  3. La méthode cree_fils_droite() est construite sur le même modèle que cree_fils_gauche().
Voir une solution

Exercice 5 : Structure d'arbre avec la classe ArbreBin

À partir de la classe précédente ArbreBin, suivez les étapes ci-dessous :

  1. Avec la méthode d'importation, créez la structure d'arbre suivante :

    arbre_liste = ["A",
                ["B", ["C",[],["E"]],
                      ["D"]],
                ["F", ["G", ["I"]],
                      ["H",["J", ["K"]]] ],
              ]

    Visualisez le résultat de cette opération avec la méthode show().

  2. Ajoutez la feuille "L" à l'arbre comme une feuille du nœud K.

    Visualisez le résultat de cette opération avec la méthode show().

  3. Quelle est la profondeur de "L" dans cet arbre ?

    Quelle méthode pouvez-vous utiliser pour calculer la profondeur d'un nœud dans un arbre ?

  4. Déterminez la hauteur de cet arbre.

    5. Voir une solution

Entraînement 6 :

A partir de la classe Arbrebin() précédente, implémenter une méthode calculant la hauteur d'un arbre binaire

Voir une solution

Entraînement 7 :Caractérisation d'un arbre

On donne ci-dessous le tableau caractérisant un arbre :

Noeud Étiquette Noeud du sous arbre gauche SAG Noeud du sous arbre droit SAD
1 * 2 3
2 + 4 5
3 - 6 7
4 3
5 / 8 9
6 8
7 * 10 11
8 4
9 2
10 2
11 3

Sans utiliser python :

  1. Représentez l'arbre correspondant à partir du tableau donné.
  2. Déterminez la hauteur de cet arbre. Comment définissez-vous la hauteur d'un arbre ?
  3. Est-ce que cet arbre est binaire et complet ? Justifiez votre réponse.
  4. Quel est le résultat de cette suite d’opérations mathématiques ?


Savoir faire

  • Savoir identifier des situations nécessitant une structure de données arborescente.
  • Savoir identifier arbres binaires, nœuds, racines, feuilles, sous-arbres gauches, sous-arbres droits.
  • Savoir évaluer quelques mesures des arbres binaires (taille, profondeur, hauteur).

Fiche de cours