Méthode « diviser pour régner »
Numérique et sciences informatiques

En première, nous avons vu deux algorithmes :
- le tri par sélection qui a une complexité quadratique dans le pire des cas, le meilleur des cas et en moyenne.
- le tri par insertion qui a une complexité linéaire dans le meilleur des cas, et quadratique dans le pire des cas et en moyenne.
Ces algorithmes voient peu voire pas du tout d'utilisation en pratique en raison de leur faible efficacité. Nous allons découvrir une méthode de tri plus performante.
Euclide a introduit la méthode du "Diviser pour Régner" au IIIe siècle avant J-C. C'est une approche algorithmique où un problème complexe est subdivisé en de multiples sous-problèmes.
Le procédé Diviser pour régner est un cas particulier de la récursivité, où la taille du problème est divisée à chaque appel récursif plutôt que seulement décrémenté d'une unité.
La méthode "Diviser pour régner" :
La méthode "Diviser pour régner" consiste, pour résoudre un problème complexe de taille N, à :
- Diviser : diviser le problème en sous-problèmes (par exemple, de taille N/2)
- Régner : résoudre ces sous-problèmes distincts (généralement de manière récursive)
- Combiner : fusionner les solutions pour obtenir la solution du problème initial
En général, cette méthode nécessite moins d'appels récursifs. Parfois, elle aboutit à un algorithme de résolution plus rapide pour certains cas.
L'idée fondamentale est que les "petits problèmes" sont souvent plus simples à résoudre que le problème initial. Une fois ces derniers résolus, leurs solutions combinées permettent d'obtenir la solution du problème d'origine.
Exemple
Pour illustrer la méthode "Diviser pour régner" avec le calcul de 2^6, on décompose le problème en deux parties égales : 2^3 et 2^3. Ensuite, chaque partie est fractionnée en deux parties égales : 2^2 et 2^1, et résolue récursivement. Enfin, les résultats sont combinés pour obtenir le résultat final.
Voici en détail les étapes pour calculer 2^6 à l'aide de cette méthode :
- Diviser le problème en deux parties égales : 2^3 et 2^3.
- Diviser chaque partie en deux parties égales : 2^2 et 2^1.
- Régner en résolvant chaque partie de manière récursive :
- 2^1 = 2
- 2^2 = 2 * 2 = 4
- 2^3 = 2^2 * 2^1 = 4 * 2 = 8
- Combiner les résultats pour obtenir le résultat final :
- 2^6 = 2^3 * 2^3 = 8 * 8 = 64
Ainsi, la méthode "Diviser pour régner" permet une résolution efficace en subdivisant le problème en sous-problèmes plus simples et en consolidant les résultats. Cette approche s'avère précieuse pour aborder des problèmes complexes comme le calcul de puissances élevées.
Implémentation en Python du “diviser pour régner”
Nous allons écrire une fonction “puissance(x,n)” basée sur ce paradigme, où x et n sont deux entiers (positif pour n). Pour cela, nous allons prendre en compte que:
- si n=0, alors xn = 1.
- si n est pair, alors x n = (xn/2)2
- si n est impair, alors x n = x * (xn/2)2
Cela donne alors la fonction suivante (exponentiation rapide):
def expo_rapide(x,n):
"""
Renvoie xn
:param: n (int) et x (int)
:return: un entier
:CU: n>=0
"""
if n == 0:
return 1
elif n % 2 == 0:
return expo_rapide(x * x,n // 2)
else:
return x*expo_rapide(x * x, n // 2)
Entraînement 1 :
Déterminer le coût, en nombre de multiplications, de l’algorithme corrigé pour n = 5, 10, 20, 50 et 100. Vous pouvez modifier la fonction expo_rapide(x,n) pour vérifier vos résultats.
| n = | 5 | 10 | 20 | 50 | 100 |
|---|---|---|---|---|---|
| nombre d'opération | 5 | 10 | 20 | 50 | 100 |
nombre d'opération avec expo_rapide(x,n) |
Le tri fusion
Le tri fusion découvert par John von Neumann en 1945 consiste à trier récursivement les deux moitiés de la liste, puis à fusionner ces deux sous-listes triées en une seule. La condition d’arrêt à la récursivité sera l’obtention d'une liste à un seul élément, car une telle liste est évidemment déjà triée.

Voici donc les trois étapes (diviser, régner et combiner) de cet algorithme :
- Diviser la liste en deux sous-listes de même taille (à un élément près) en la "coupant" par la moitié.
- Trier récursivement chacune de ces deux sous-listes. Arrêter la récursion lorsque les listes n'ont plus qu'un seul élément.
- Fusionner les deux sous-listes triées en une seule.
On considère la liste suivante de sept entiers :

On la scinde en deux sous-listes en la coupant par la moitié :
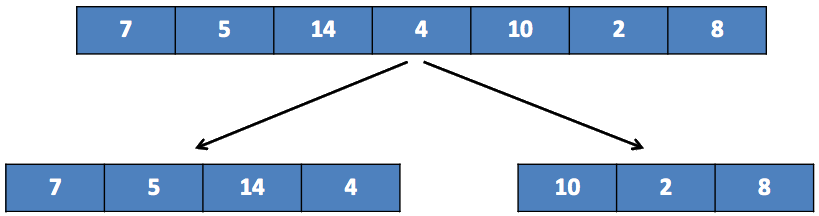
Sous-listes que l’on scinde à leur tour :
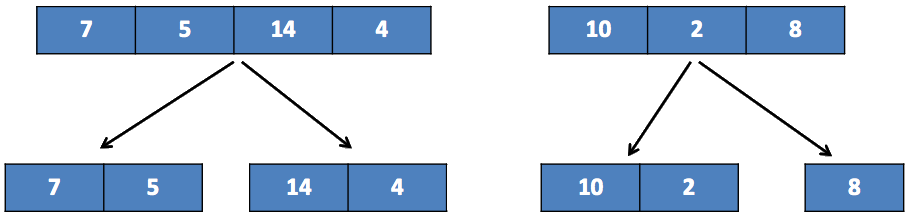
Sous-listes que l’on scinde à leur tour :
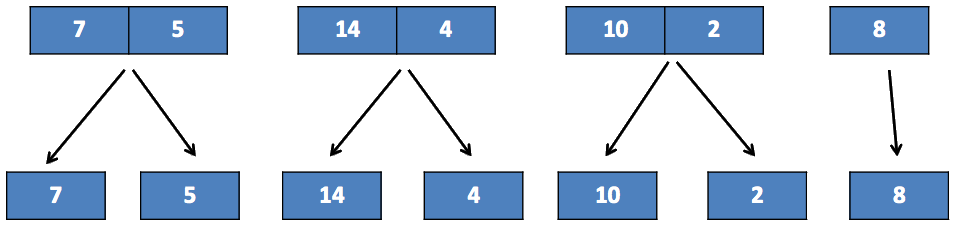
Ces sous-listes sont triées car elles n’ont qu’un élément. On va maintenant les fusionner deux par deux en de nouvelles sous-listes triées :
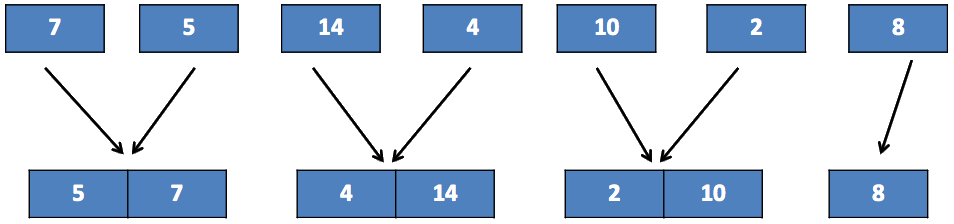
De nouveau une étape de fusionnement :
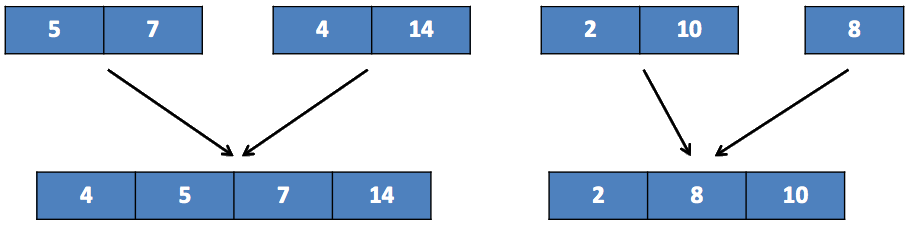
Une dernière fusion :
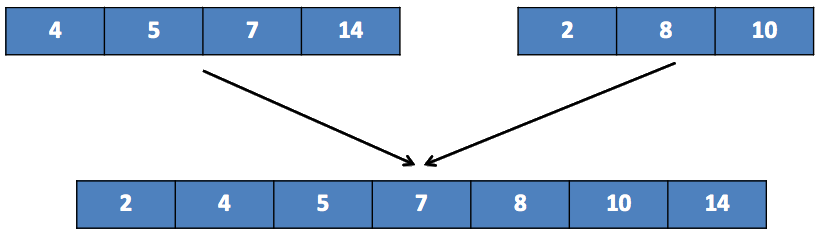

La fusion se fait principalement grâce aux 3 étapes suivantes :
- La comparaison des plus petites valeurs non triées du tableau
- L’affectation de la plus petite valeur au nouveau tableau trié
- La translation de l’indice du tableau contenant cette valeur
On a fusionné toutes les sous-listes obtenues lors des appels récursifs, le tri est terminé :

Regardons l'algorithme de fusion de deux tableaux triés.
FONCTION fusion (tab1, tab2)
// tab1 et tab2 sont deux tableaux triés
// Initialisation
pos1 <- 0 // marqueur de position du 1er tableau
pos2 <- 0 // marqueur position du 2ème tableau
resultat <- [] // liste vide destinée à accueillir les éléments triés
// Boucle
TANT QUE l'on a pas atteint la fin d'un des tableaux
SI tab1[pos1] <= tab2[pos2] ALORS
Insérer tab1[pos1] à la fin de resultat
incrémenter pos1
SINON
Insérer tab2[pos2] à la fin de resultat
incrémenter pos2
FIN SI
FIN TANT QUE
// Finalisation
Insérer les éléments restants du tableau non vide à la fin de resultat
RENVOYER resultatEt voici l'algorithme récursif de tri fusion qui utilise la fonction fusion définie précédemment..
FONCTION tri_fusion (tab)
n <- Longueur de tab
// Cas de base
SI n == 1 ALORS
RENVOYER tab
FIN SI
// Recursion sur les deux demi-tableaux
SINON
# Diviser
t1 <- tab[:n//2]
t2 <- (tab[n//2:]
# Régner
t1_tri <- tri_fusion(tab[:n//2]
t2_tri <- tri_fusion(tab[n//2:]
# Combiner
resultat <- fusion(t1_trie, t2_trie)
// Renvoi des la fusion des deux tableaux
RENVOYER resultatIl s'agit de la meilleure complexité que puisse avoir un algorithme de tri.
Entraînement 2 :
- Réaliser le schéma en arborescence permettant le tri du tableau suivant [19,4,7,6,9,8,10,2,1,3] avec l’algorithme de tri fusion («diviser pour régner»)2.
- Quel est l’avantage de l’algorithme de tri fusion par rapport aux algorithmes de tri vus en classe de 1ère ?
- A partir des algorithmes, implémenter un programme en python afin de tester le tableau de la question 1 (Ne pas oublier de commenter et d'ajouter le docstring au code).
Comparons avec les tris connus:
| Nom | Complexité | Coût en opération pour un tableau de 10^8 valeurs (assez fréquent dans les grandes entreprises) |
Durée pour un ordinateur cadencé à 3GHz nécessitant 10 cycles pour une comparaison |
|---|---|---|---|
| Tri par sélection | n^2 | (10^8)2 = 1016 | approx 381 jours |
| Tri par insertion | n2 | (108)2 = 1016 | approx 381 j |
| Tri Fusion | n*log2(n) | (108)*log2(108) = 2,7.109 | 9s |
Entraînement 3 :Recherche dichotomique d'un tableau trié
Nous avons vu en première la recherche dichotomique d'un tableau trié de façon itérative. Nous allons voir cet algorithme de recherche de façon récursive.
On cherche l'élément element dans le tableau T . La fonction rech_dicho(element, tableau) créée devra renvoyer True si l'élément cherché est dans le tableau, False sinon.
L'idée de cet algorithme récursif est la suivante:
Si l'élément du milieu du tableau T est égal à el alors on retourne True Sinon on effectue la recherche sur le sous-tableau de gauche ou de droite.
- Quel sera le cas d'arrêt de cet algorithme ?
- Implémenter cet algorithme de façon récursive.
- Écrire une fonction
rech_dicho_position(element, tableau)récursive de la recherche dichotomique qui renvoie l'indice si ce dernier est dans le tableau, False sinon.
Savoir faire
- Savoir écrire un algorithme utilisant la méthode « diviser pour régner ».
- Savoir décomposer un problème en tâches plus simples et indépendantes
- Savoir combiner les résultats de plusieurs fonctions pour obtenir un résultat final
Fiche de cours