Informatique au lycée Faustin Fleret

Les graphes :

Problème des 7 ponts de Könisgberg, Euler, 1736

La notion de graphes semble apparaître pour la première fois dans un article du mathématicien suisse Leonhard Euler parut en 1735, dans lequel il se penchait sur le “problème des ponts de Königsberg”, ville représentée avec ses ponts sur le schéma ci-dessus.

On parle de chaîne eulérienne lorsque toutes les arêtes sont présentes qu'une seule fois et on parle de circuit hamiltonien quand tous les sommets sont présents qu'une seule fois.

De manière générale, un graphe permet de représenter les connexions d’un ensemble en exprimant les relations entre ses éléments : réseau de communication, réseau routier, . . . , mais aussi relations sociales ou interactions entre espèces animales.

La théorie des graphes est une branche déjà ancienne des mathématiques (le fameux problème des ponts de Königsberg d’Euler date de 1736). Néanmoins, c'est un domaine incontournable de l’informatique actuellement.
Les informaticiens cherchent à concevoir des algorithmes efficaces pour résoudre les problèmes faisant intervenir un graphe (recherche du plus court chemin, problème du voyageur de commerce (PVC), recherche d’un arbre couvrant, . . .).
Le programme de Terminale prévoit d'en aborder quelques aspects, essentiellement de nature algorithmique.

Exemples d'utilisation des Graphes

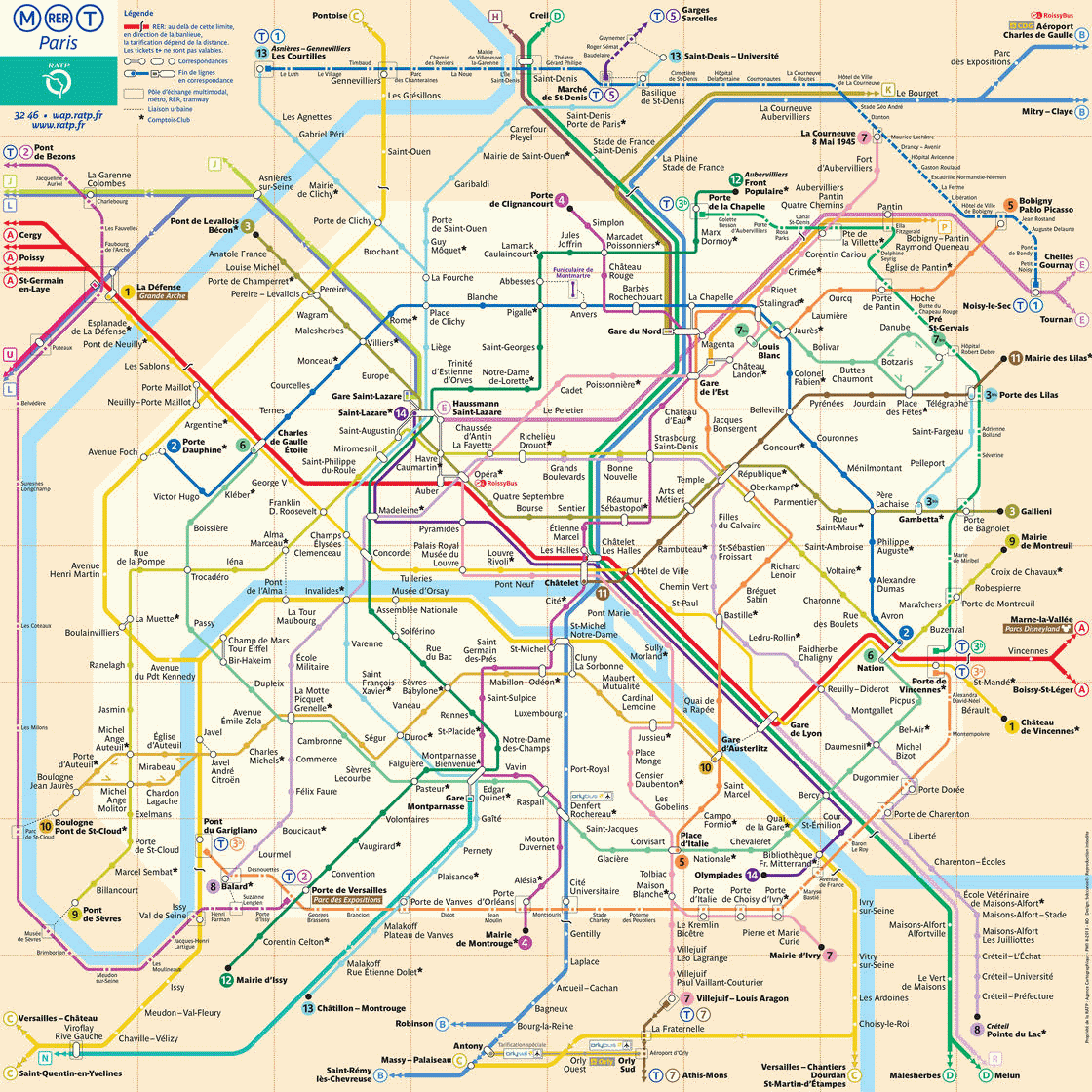
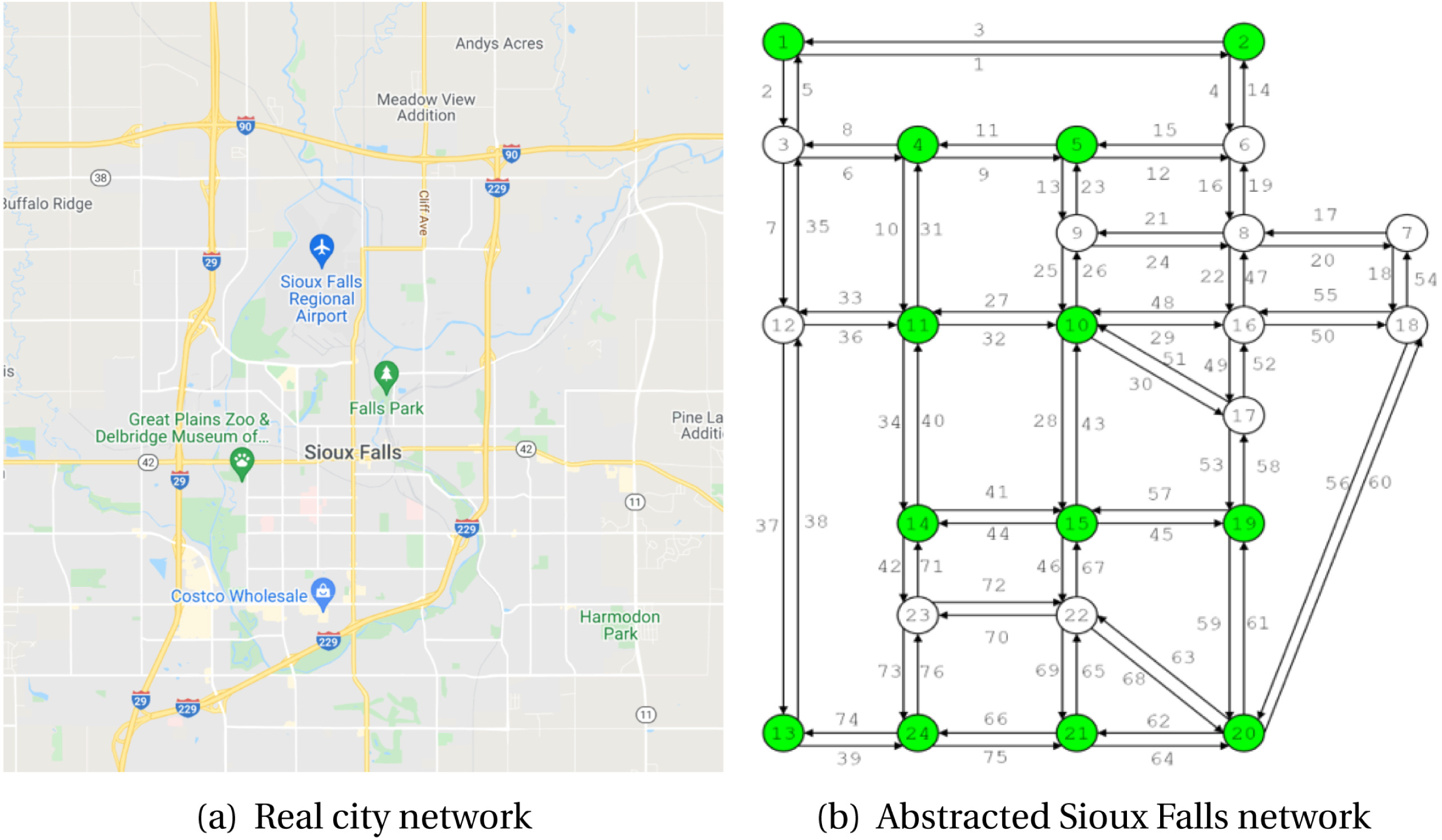
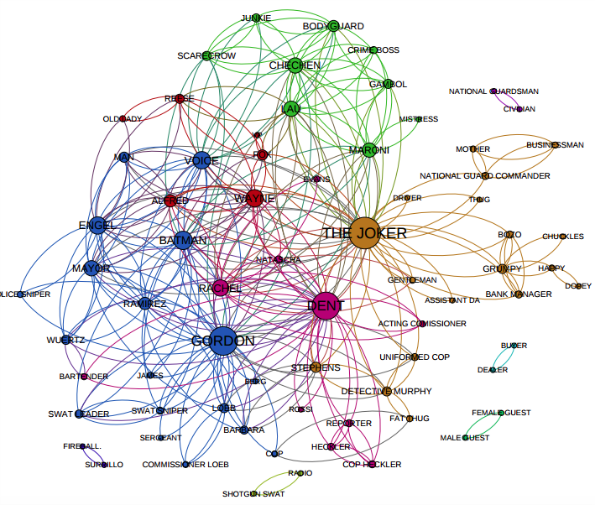
Définition :

Un graphe G = (V, E) est défini par l’ensemble fini V = {v1,v2,...,vn} dont les éléments sont appelés sommets (vertices en anglais), et par l’ensemble fini E = {e1,e2,...,em} dont les éléments sont appelés arêtes (edges en anglais).

• Une arête e de l’ensemble E est définie par une paire non ordonnée de sommets, appelés les extrémités de e. Si l’arête e relie les sommets a et b, on dira que ces sommets sont adjacents (ou incidents avec e).
• on appelle ordre d’un graphe le nombre de sommets n de ce graphe.
• Le degré d’un sommet est le nombre de sommets qui lui sont adjacents, et le degré d’un graphe le degré maximum de tous ses sommets.

Les graphes tirent leur nom du fait qu’on peut les représenter graphiquement : à chaque sommet de G on fait correspondre un point du plan et on relie les points correspondant aux extrémités de chaque arête. Il existe donc une infinité de représentations possibles.

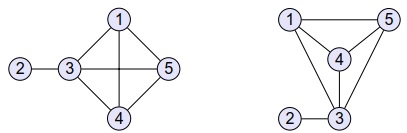
G est un graphe d’ordre 5 ; il possède un sommet de degré 1 (le sommet 2), trois sommets de degré 3 (les sommets 1, 4 et 5) et un sommet de degré 4 (le sommet 3).

Entraînement 1 :

Représenter le graphe décrit par les ensembles V et E :
V = {A, B, C, D, E, F} et E = {(A, B), (A, C), (B, C), (B, E), (C, A), (C, D), (D, A), (D, E), (E, F), (F, D)}

Entraînement 2 :

Considérons le graphe G suivant :

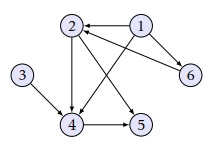
1. Déterminer la représentation V et E du graphe G = (V, E)
Voir une solution

Solution

le graphe G est défini par V = {1,2,3,4,5,6} et E = {(1,2),(1,4),(1,6),(2,4),(2,5),(3,4),(4,5),(6,2)
Masquer

Deux méthodes permettent de représenter un graphe :

• à l’aide de listes d’adjacence (à chaque sommet on associe la liste de ses voisins) ;
• à l’aide de matrices d’adjacence (le coefficient d’indice (i,j) traduit l’existence ou non d’une liaison entre deux sommets).

Listes adjacence

Une manière de représenter un graphe est la liste d'adjacence. Dans cette représentation, on utilise une liste pour chaque sommet, qui contient les sommets adjacents. Si le graphe est pondéré, chaque élément de la liste peut être une paire (valeur, sommet_adjacent).

On peut représenter un graphe comme un dictionnaire, où les clés sont les sommets et les valeurs, les sommets reliés aux clés.

#liste d’adjacence avec les dictionnaires python
G = {
1:[2, 4, 6], # voisins de 1
2:[4, 5], # voisins de 2
3:[4], # voisins de 3
4:[5], # voisins de 4
5:[], # voisins de 5
6:[2], # voisins de 6
}

Matrices d'adjacence

La matrice d'adjacence est une représentation sous forme de tableau où chaque élément (i,j) représente la présence ou l'absence d'une arête entre les sommets i et j. Si le graphe est pondéré , chaque élément (i,j) représente le poids de l'arête entre i et j.

Quand deux sommets i et j sont reliés par une arêtes, on met un “1” à l’intersection de la ligne i et de la colonne j. Dans le cas contraire, on met un “0”.
La matrice d'adjacence d'un graphe non orienté est symétrique, c'est-à-dire qu'elle ne change pas si on échange ses lignes et ses colonnes.

Représentation avec python :

import numpy as np
G=np.array(
[[0,1,0,1,0,1],[0,0,0,1,1,0],[0,0,0,1,0,0],[0,0,0,0,1,0],[0,0,0,0,0,0],[0,1,0,0,0,0]])

Entraînement 3:

Représenter la matrice d'adjacence de G avec G = {A : [B, C], B : [A, C, E, F], C : [A, B, D], D : [C, E], E : [B, D, F], F : [B, E]}

Entraînement 4 :

Considérons le graphe G suivant :
On considère le graphe suivant :graph G {1 -- 2 ;1 -- 4 ;2 -- 3 ;3 -- 1 ;4 -- 2 ;}

1. Un graphe est dit complet si tous ses sommets sont reliés
   G est-il complet ?
2. Est-ce un graphe simple ou orienté ?
3. Quels sont les voisins de 1?
4. Construire sa matrice d’adjacence.

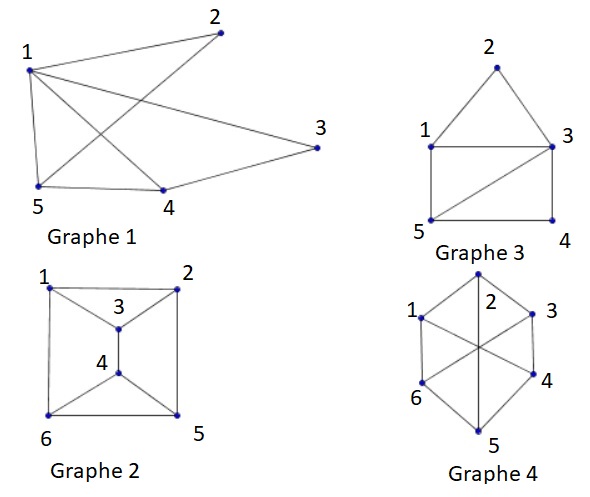
Entraînement 5 :

Parmi les graphes ci-dessous :

1. lesquels sont orienté ?
2. lesquels représentent le même graphe ?
   Voir une solution

   Solution

   Réaliser les matrices d’adjacence des 4 graphes pour comparer. Masquer

Pour compléter ce cours, voici l'excellente vidéo de Roland Leguizammon qui résume très bien toutes ces notions.

Un graphe n’est autre qu’une représentation d’une situation; c’est donc un objet abstrait… Et en informatique, il existe un paradigme de programmation permettant d’implémenter de telles notions : la Programmation Orientée Objet (La POO).

Pour créer un graphe, nous pourrions avoir besoin de :

• Créer un graphe (vide ou à partir d’une liste de sommets),
• Ajouter un sommet,
• Ajouter une arête,•supprimer un sommet,
• Supprimer une arête,
• Le graphe est-il vide ?
• Quels sont les sommets adjacents à un sommet donné ?
• Retourner la matrice d’adjacence d’un graphe,
• Créer un graphe à partir d’une matrice d’adjacence.
• ...

Voici un exemple de la représentation de la classe Graphe en python.

class Graphe(object):
    """Classe représentant un graphe.

    Un graphe est représenté par un dictionnaire.
    """
    def __init__(self):
        """Initialise le graphe à vide.
        """
        self.graphe = {}

    def ajouteSommet(self, sommet):
        """Ajoute un sommet au graphe sans aucun voisin.
        """
        if sommet not in self.graphe.keys():
            self.graphe[sommet] = {}

    def ajouteArrete(self, sommet, sommetVoisin, p):
        """Crée une arrête en reliant sommet avec sommetVoisin en associant le poids p.
        """
        if sommet != sommetVoisin:
            try:
                self.graphe[sommetVoisin][sommet] = p
                self.graphe[sommet][sommetVoisin] = p
            except KeyError:
                pass

    def supprimeSommet(self, sommet):
        """Supprime un sommet du graphe.
        """
        for sommetVoisin in self.graphe[sommet].keys():
            del self.graphe[sommetVoisin][sommet]
        del self.graphe[sommet]

    def supprimeArrete(self, sommet, sommetVoisin):
        """Supprime une arrête.
        """
        if sommet in self.graphe[sommetVoisin]:
            self.supprimeSommet(sommet)
            self.supprimeSommet(sommetVoisin)

    def toMatrice(self):
        """Affichage matriciel du graphe.
        """
        print (" "),
        for i in sorted(self.graphe.keys()):
            print (i),
        print()
        for i in sorted(self.graphe.keys()):
            print (i),
            for j in sorted(self.graphe.keys()):
                if i in self.graphe[j].keys():
                    print ('1'),
                else:
                    print ('0'),
            print()

    def toListe(self):
        """Affiche le graphe sous forme de listes d'adjacences.
        """
        for i in sorted(self.graphe.keys()):
            print (i), " --> ",
            print (self.graphe[i].keys())
            
if __name__ == "__main__":
    # Point d'entrée en exécution.
    graph = Graphe()
    graph.ajouteSommet('A')
    graph.ajouteSommet('B')
    graph.ajouteSommet('C')
    graph.ajouteSommet('D')
    graph.ajouteSommet('E')
    graph.ajouteSommet('F')

    graph.ajouteArrete('A', 'C', 2)
    graph.ajouteArrete('D', 'B', 2)
    graph.ajouteArrete('B', 'C', 800)
    graph.ajouteArrete('B', 'D', 7)
    graph.ajouteArrete('C', 'D', 7)
    graph.ajouteArrete('F', 'A', 7)
    print (graph)
    print()
    graph.toMatrice()
    print()
    graph.toListe()
    print()

# Entraînement 7
def matrice_adj_vers_liste(matrice):
    """
    matrice - list, tableau 2D représentant une matrice d'adjacence associée à un graphe (orienté ou non)
    Sortie: dico - dictionnaire tel que:
                   les clefs sont les numéros associés aux sommets du graphe
                   les valeurs sont un tableau des voisins (ou successeurs) du sommet
    """

assert (matrice_adj_vers_liste([[0, 1, 1, 0, 0], [1, 0, 0, 0, 1], [1, 0, 0, 1, 1], [0, 0, 1, 0, 1], [0, 1, 1, 1, 0]])
== {0: [1, 2], 1: [0, 4], 2: [0, 3, 4], 3: [2, 4], 4: [1, 2, 3]})

# Entraînement 8
def liste_vers_matrice_adj(dico):
    """
    dico - dictionnaire tel que:
                les clefs sont les numéros associés aux sommets d'un graphe (orienté ou non)
                les valeurs sont un tableau des voisins (ou successeurs) du sommet
    Sortie: matrice - tableau 2D représentant la matrice d'adjacence associée au graphe
    """

assert ( liste_vers_matrice_adj({0: [1, 2], 1: [0, 4], 2: [0, 3, 4], 3: [2, 4], 4: [1, 2, 3]})
          == [[0, 1, 1, 0, 0],
              [1, 0, 0, 0, 1],
             [1, 0, 0, 1, 1],
              [0, 0, 1, 0, 1],
             [0, 1, 1, 1, 0]])

# Entraînement 9
def dico_vers_matrice_pond(dico):
    """
    dico - dictionnaire tel que:
                les clefs sont les numéros associés aux sommets d'un graphe pondéré non orienté
                les valeurs sont un dictionnaire {voisins: pondération } du sommet
    Sortie: matrice - tableau 2D représentant une matrice de pondération associée au graphe
    """

assert (dico_vers_matrice_pond({0: {2: 3, 3: 1}, 1: {2: 4, 3: 2, 4: 1}, 2: {0: 3, 1: 4, 3: 6}, 3: {0: 1, 1: 2, 2: 6, 4: 5}, 4: {1: 1, 3: 5}})
        == [[0, 0, 3, 1, 0],
            [0, 0, 4, 2, 1],
            [3, 4, 0, 6, 0],
            [1, 2, 6, 0, 5],
            [0, 1, 0, 5, 0]])

# Entraînement 10
def matrice_pond_vers_dico(matrice):
    """
    matrice - list, tableau 2D représentant une matrice de pondération associée à un graphe pondéré
    Sortie: dico - dictionnaire tel que:
                   les clefs sont les numéros associés aux sommets du graphe
                   les valeurs sont un dictionnaire {voisins: pondération} du sommet
    """

assert (matrice_pond_vers_dico([[0, 0, 3, 1, 0], [0, 0, 4, 2, 1], [3, 4, 0, 6, 0], [1, 2, 6, 0, 5], [0, 1, 0, 5, 0]])
            == {0: {2: 3, 3: 1},
                1: {2: 4, 3: 2, 4: 1},
                2: {0: 3, 1: 4, 3: 6},
                3: {0: 1, 1: 2, 2: 6, 4: 5},
                4: {1: 1, 3: 5}})

def est_symetrique(matrice):
    """
    matrice - list, tableau 2D d'entiers représentant une matrice carrée
    Sortie: bool - True si la matrice est symétrique, False sinon
    """

assert (est_symetrique([[0, 1, 1, 0, 0], [1, 0, 0, 0, 1], [1, 0, 0, 1, 1], [0, 0, 1, 0, 1], [0, 1, 1, 1, 0]])
        == True)
assert (est_symetrique([[0, 1, 1, 0, 0], [0, 0, 1, 0, 1], [1, 0, 0, 0, 1], [1, 0, 1, 0, 1], [0, 1, 1, 1, 0]])
        == False)

def est_pondere(matrice):
    """
    matrice - list, tableau 2D d'entiers représentant une matrice carrée
    Sortie: bool - True si la matrice comporte des valeurs autre que 0 ou 1,
                   False sinon
    """

assert (est_pondere([[0, 1, 1, 0, 0], [1, 0, 0, 0, 1], [1, 0, 0, 1, 1], [0, 0, 1, 0, 1], [0, 1, 1, 1, 0]])
        == False)
assert (est_pondere([[0, 0, 3, 1, 0], [0, 0, 4, 2, 1], [3, 4, 0, 6, 0], [1, 2, 6, 0, 5], [0, 1, 0, 5, 0]])
        == True)