Informatique au lycée Faustin Fleret

Qu’est ce que la sécurité ?

La sécurité détermine les parties critiques à protéger et les risques sur le réseau.

Principes généraux

La cryptographie est une des disciplines de la cryptologie s'attachant à protéger des messages (assurant confidentialité, authenticité et intégrité) en s'aidant de clés. Elle se distingue de la stéganographie qui fait passer inaperçu un message dans un autre message alors que la cryptographie rend un message supposément inintelligible à autre que qui-de-droit.
Elle est utilisée depuis l'Antiquité, mais certaines de ses méthodes les plus modernes, comme la cryptographie asymétrique, datent de la fin du xxe siècle.

Sécuriser un réseau, c'est assurer :

• La confidentialité des données (et des acteurs) de la communication ;
• L'authenticité des données de la communication en vérifiant l’identité des acteurs ;
• l'intégrité des données en vérifiant qu'elles n’ont pas été altérées ;
• La disponibilité de la communication
• la "non-répudiation" : les acteurs impliqués dans la communication ne peuvent nier y avoir participer.

La cryptologie est « science du secret ».

Le chiffrement est le procédé de cryptographie. Son but est de rendre un document incompréhensible par une personne qui n'a pas à connaître son contenu. On chiffre (cipher en anglais) un message avec une "clé de chiffrement". Un message qui a été chiffré est ensuite déchiffré par la personne qui a la clé de chiffrement.

Décrypter un message est le fait de tenter, SANS la clé de déchiffrement, de retrouver le message original.

Le chiffrement à clé symétrique

Le chiffrement symétrique est un algorithme de chiffrement qui utilise la même clé pour chiffrer et déchiffrer les données. Cette clé est partagée entre les parties qui communiquent et elle doit être gardée secrète pour assurer la sécurité de la communication. L'algorithme de chiffrement symétrique le plus communément utilisé est l'algorithme AES (Advanced Encryption Standard).

Lorsqu'un message est envoyé à un destinataire, le message est chiffré en utilisant la clé symétrique partagée. Le destinataire doit utiliser la même clé pour déchiffrer le message. La sécurité du chiffrement symétrique dépend de la sécurité de la clé partagée.

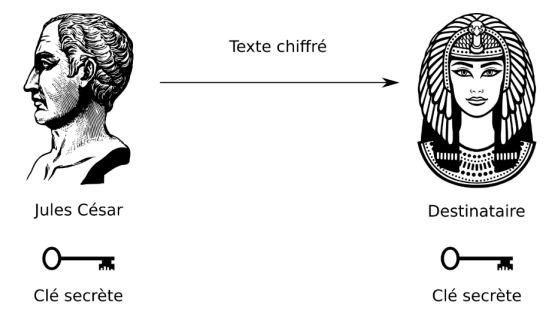
Entraînement 1 : le code de César

L’exemple le plus connu de chiffrement symétrique, et un des plus simples, est le chiffre de César. Pour obtenir le texte chiffré, le chiffre de César consiste à remplacer chaque lettre du texte en clair par la lettre obtenue après un décalage d’un nombre fixe de lettres dans l’alphabet.
Pour un décalage de 3 lettres, le A devient D, le B devient E… Comme le montre l’image ci-dessous :

Le nombre 3, qui correspond au nombre de lettres à décaler, est appelé la clef secrète de chiffrement. Pour déchiffrer le message, il suffit de donner la clef de chiffrement au destinataire du message qui réalise l’opération inverse pour déchiffrer le message.

La fonction position_alphabet ci-dessous prend en paramètre un caractère lettre et renvoie la position de lettre dans la chaîne de caractères ALPHABET s’il s’y trouve et -1 sinon.
La fonction cesar prend en paramètre une chaîne de caractères message et un nombre entier décalage et renvoie le nouveau message codé avec le codage de César utilisant le décalage .

Copier le code

ALPHABET = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'

def position_alphabet(lettre):
    # lettre.upper() convertit la lettre en majuscule
    return ALPHABET.find(lettre.upper())

def cesar(message, decalage):
    resultat = ...
    for lettre in message:
        if lettre.isalpha():  # Vérifie si la lettre est alphabétique
            indice = (position_alphabet(...) + ...) % 26
            # lettre.isupper() vérifie si la lettre était en majuscule
            if lettre.isupper():
                resultat += ALPHABET[...]
            else:
                resultat += ALPHABET[...].lower()
        else:
            resultat += ...
    return ...

Compléter la fonction cesar.
Exemples :

Copier le code

# Résultat attendu : 'FSRNSYV E XSYW. ZMZI PE QEXMIVI RWM !'
print(cesar('BONJOUR A TOUS. VIVE LA MATIERE NSI !', 4))

# Résultat attendu : 'BONJOUR A TOUS. VIVE LA MATIERE NSI !'
print(cesar('GTSOTZW F YTZX. ANAJ QF RFYNJWJ SXN !', -5))

Entraînement 2 :

Décrypter le message suivant (code cesar)

RWM IX XSXS RI WI WITEVIRX NEQEMW !

Entraînement 3 : Analyse fréquentielle

Dans la langue française, la lettre "E" est la plus employée. Des études statistiques ont permis d'estimer la fréquence des lettres en fonction de la langue. Voici ce tableau de fréquences pour le français et l'anglais.

Fréquences des lettres

Lettre	Fréquence (Français)	Fréquence (Anglais)
A	7.11%	8.04%
B	0.94%	1.49%
C	3.48%	2.54%
D	3.73%	4.25%
E	17.26%	12.49%
F	0.84%	2.40%
G	1.18%	1.99%
H	0.85%	6.09%
I	6.86%	7.57%
J	0.45%	0.53%
K	0.05%	0.74%
L	3.87%	4.03%
M	3.15%	2.51%
N	6.69%	7.23%
O	5.95%	7.64%
P	3.03%	1.93%
Q	0.65%	0.12%
R	6.07%	5.99%
S	5.68%	6.51%
T	5.48%	9.28%
U	5.41%	2.76%
V	0.90%	1.05%
W	0.04%	2.24%
X	0.15%	0.14%
Y	0.04%	1.97%
Z	0.30%	0.09%
-	0.01%	0.01%
,	0.01%	0.01%
.	0.01%	0.01%
;	0.01%	0.01%
'	0.01%	0.01%
:	0.01%	0.01%
?	0.01%	0.01%
!	0.01%	0.01%

Si on connaît la langue d'un texte, alors on peut par exemple, dans le cas d'un chiffrement de César, retrouver le décalage.
Pour que cette analyse soit efficace, il faut que le texte soit suffisamment long.

1. Écrire une fonction, `analyse_frequence`, qui renvoie un dictionnaire des fréquences en pourcentages des différentes lettres utilisées dans un message passé en argument.

>>> analyse_frequence("hello world")
{'h': 10.0, 'e': 20.0, 'l': 30.0, 'o': 20.0, 'w': 10.0, 'r': 10.0, 'd': 0.0}

2. Effectuez une analyse fréquentielle du fichier suivant.
3. En déduire, dans le cas d'utilisation du code César, la clé utilisée pour ce texte.
4. Que venez-vous de décoder ?

Entraînement 3 : Le chiffrement XOR (ou exclusif)

Harry Potter souhaite envoyer un message secret à Hermione Granger en utilisant une forme spéciale de cryptographie magique. Le message original est constitué de la représentation binaire ASCII du nom "Voldemort".

Copier le code

Message original (Voldemort en ASCII) : 
01010110 01101111 01101100 01100100 01100101 01101101 01101111 01110010 01110100

Harry choisit une séquence binaire magique comme clé de chiffrement :

Copier le code

Clé magique :
10100111 11001101 01010101 11100010 11010110 00111101 10101011 01010011 01101101 11001010

Harry et Hermione savent qu'ils peuvent introduire une touche de magie XOR dans le processus en utilisant des sorts spéciaux.

• Harry chiffre le message original en appliquant une opération magique XOR entre chaque séquence binaire du message original et de la clé magique. Il envoie le message enchanté à Hermione.
• Hermione reçoit le message enchanté et utilise la même séquence binaire magique pour effectuer l'opération magique XOR inverse et récupérer le message original.

	M	E	S	S	A	G	E
Codes ASCII	77	69	83	83	65	71	69
Message en binaire	01001101	01000101	01010011	01010011	01000001	01000111	01000101
XOR	⊕	⊕	⊕	⊕	⊕	⊕	⊕
Clé en binaire	01000011	01001100	01000101	01000011	01001100	01000101	01000011
=	=	=	=	=	=	=	=
Message crypté en binaire	00001110	00001001	00010110	00010000	00001101	00000010	00000110

Écrire une fonction decryptage_xor qui prend en paramètre un message et une clé, et renvoie le nouveau message décrypté avec le codage utilisant le XOR. Quel est le nouveau message enchanté que Harry envoie à Hermione ?

Copier le code

Message original crypté (en ASCII) : 
11000111 10101101 01010100 10011001 00100110 11101110 00101111 01010011

Copier le code

Clé magique :
10101010 11001100 00110011 11110000 01010101 10011001 01001010 00111100

Vous avez à votre disposition les codes suivant pour vous aider :

Copier le code

def binaire_vers_ascii(chaine_binaire):
    """
    Convertit une chaîne binaire en ASCII.
    Argument : chaine_binaire (str): La chaîne binaire à convertir en ASCII.
    Return : str: La représentation ASCII de la chaîne binaire.
    """
    # Assurer que la chaîne binaire est divisible par 8
    chaine_binaire = chaine_binaire.zfill((len(chaine_binaire) // 8 + 1) * 8)

    # Découper la chaîne binaire en octets de 8 bits
    octets = [chaine_binaire[i:i+8] for i in range(0, len(chaine_binaire), 8)]

    # Convertir chaque octet en entier puis en caractère ASCII
    caracteres_ascii = ''.join([chr(int(octet, 2)) for octet in octets])

    return caracteres_ascii

# Exemple d'utilisation
chaine_binaire = "010101100110111101101100011001000110010101101101011011110111001001110100"
ascii_resultat = binaire_vers_ascii(chaine_binaire)

print(f"ASCII résultat : {ascii_resultat}")

Voir une solution

Solution

Copier le code

def decryptage_xor(message_crypte, cle_magique):
    """
    Décrypte un message chiffré en utilisant l'opération XOR.
    Arguments:
    - message_crypte (str): Le message chiffré en binaire.
    - cle_magique (str): La clé de chiffrement en binaire.
    Return:
    str: Le message original décrypté en binaire.
    """

    # Assurer que les deux chaînes ont la même longueur
    min_length = min(len(message_crypte), len(cle_magique))
    message_crypte = message_crypte[:min_length]
    cle_magique = cle_magique[:min_length]

    # Appliquer l'opération XOR bit à bit
    message_decrypte = ""
    for i in range(min_length):
        bit_message = int(message_crypte[i])
        bit_cle = int(cle_magique[i])
        message_decrypte += str(bit_message ^ bit_cle)

    return message_decrypte

# Exemple d'utilisation
message_crypte = "11000111101011010101001001100111001011001110110000010011101110001011101001011"
cle_magique = "1010101011001100001100111110000010101011001100100101000111100"

message_decrypte = decryptage_xor(message_crypte, cle_magique)

print(f"Message original décrypté : {message_decrypte}")

Masquer

Le chiffrement à clé asymétrique

Le chiffrement asymétrique est une méthode de chiffrement qui utilise deux clés différentes pour chiffrer et déchiffrer les données. Ces clés sont appelées clé privée et clé publique. La clé privée est gardée secrète par son propriétaire, tandis que la clé publique est accessible à tous.

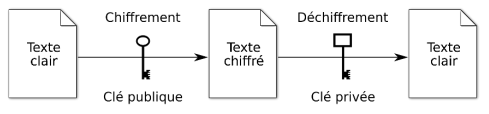
Le destinataire d'un message utilise sa clé publique pour chiffrer le message avant de l'envoyer au propriétaire de la clé privée. Le propriétaire de la clé privée utilise sa clé pour déchiffrer le message. Le chiffrement asymétrique est plus sûr que le chiffrement symétrique car la clé privée n'est connue que par le propriétaire, ce qui rend la communication plus sécurisée.

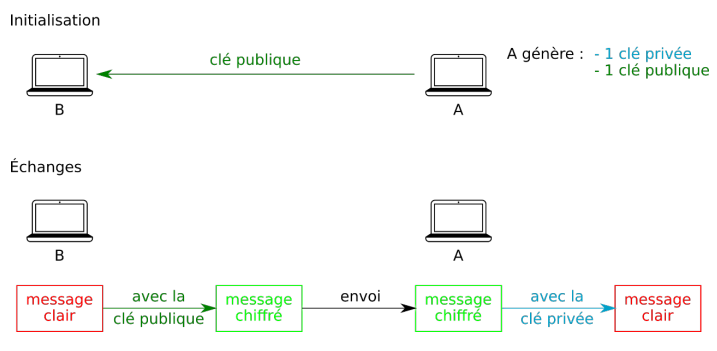
L'algorithme de chiffrement asymétrique le plus couramment utilisé est RSA.

Le chiffrement RSA (algorithmes de chiffrement asymétrique avec clés partagées)

Dans le protocole RSA, mis au point par Ron Rivest, Adi Shamir et Leonard Adleman en 1977, l'échange de clés se différencie du chiffrement symétrique. RSA est un algorithme de chiffrement asymétrique largement utilisé pour assurer la confidentialité des échanges de données sur les réseaux informatiques. Découvrons comment fonctionne cet échange de clés dans le protocole RSA.

Le chiffrement RSA repose sur le principe de la factorisation d'un grand nombre entier en produits de deux nombres premiers. Concrètement, l'algorithme utilise une paire de clés : une clé publique pour chiffrer les données et une clé privée pour déchiffrer les données.

Pour simplifier, les codes de type RSA exploitent l'idée qu'il est facile de multiplier des nombres premiers entre eux, mais difficile de faire l'opération inverse : retrouver les deux nombres premiers qui ont été multipliés pour obtenir le produit. Cette difficulté augmente considérablement lorsque l'on travaille avec des nombres premiers de plusieurs centaines de chiffres !

Il est important de rappeler que les nombres premiers, tels que 2, 3, 5, 7, 11, etc., n'ont que deux diviseurs distincts (1 et eux-mêmes). La sécurité de l'algorithme RSA dépend de la longueur des clés utilisées. Plus la clé est longue, plus elle est sécurisée face aux tentatives de déchiffrement par force brute ou par d'autres méthodes.

Le chiffrement RSA est un algorithme de chiffrement asymétrique inventé par Ron Rivest, Adi Shamir et Leonard Adleman en 1977 (nommé par les initiales de ses trois inventeurs). Il est largement utilisé pour protéger la confidentialité des échanges de données sur les réseaux informatiques.

Le chiffrement RSA repose sur le principe de la factorisation d'un grand nombre entier en produits de deux nombres premiers. L'algorithme utilise une paire de clés : une clé publique pour chiffrer les données et une clé privée pour déchiffrer les données.

Le protocole HTTPS

Le protocole HTTPS (Hypertext Transfer Protocol Secure) est une version sécurisée du protocole HTTP, utilisé pour les communications entre un client (comme un navigateur web) et un serveur web. Il utilise le chiffrement pour protéger les données qui transitent entre le client et le serveur.

Le chiffrement est réalisé à l'aide d'un certificat SSL/TLS (Secure Sockets Layer/Transport Layer Security). Ce certificat est un fichier électronique qui associe une clé publique à une entité (comme un site web). Il est émis par une autorité de certification de confiance, qui garantit que le site web est authentique et que la communication est sécurisée.

Le protocole HTTPS utilise un échange de clés pour établir une session sécurisée entre le client et le serveur. Ce processus est réalisé en plusieurs étapes :

1. Le client envoie une demande de connexion sécurisée au serveur.
2. Le serveur répond en envoyant son certificat SSL/TLS au client, qui contient la clé publique du serveur.
3. Le client vérifie la validité du certificat SSL/TLS en le comparant avec une liste de certificats de confiance, stockée dans le navigateur web.
4. Si le certificat SSL/TLS est valide, le client génère une clé de session aléatoire et l'envoie au serveur, chiffrée à l'aide de la clé publique du serveur.
5. Le serveur déchiffre la clé de session à l'aide de sa clé privée, et utilise cette clé pour chiffrer les données échangées entre le client et le serveur pendant la session.

Une fois la session établie, toutes les données échangées entre le client et le serveur sont chiffrées à l'aide de la clé de session, ce qui garantit la confidentialité et l'intégrité des données.

En conclusion, le protocole HTTPS est essentiel pour garantir la sécurité des communications sur Internet, en particulier lorsqu'il s'agit de transactions financières, de transfert de données sensibles ou de l'échange d'informations personnelles. Les sites web qui utilisent HTTPS sont facilement reconnaissables grâce au cadenas vert affiché dans la barre d'adresse du navigateur web.

Un certificat numérique possède trois caractéristiques essentielles :

• il est infalsifiable : il est chiffré pour empêcher toute modification.
• il est nominatif : il est délivré à une seule entité (comme la carte d’identité est délivrée à une personne et une seule).
• il est certifié : il y a le « tampon » de l’autorité qui l’a délivré.