Écriture d'un entier positif
Numérique et sciences informatiques

1800 av J.C
Les babyloniens définissent la notion de numération.
IVè siècle
En inde apparaît le système décimal et le zéro permettant les calculs.
XVIIè siècle
Leibnitz définie la numération binaire.
1948
John Tukey crée le terme bit contraction des mots anglais binary digit qui signifient "chiffre binaire".
I. Le système décimal
Le système décimal est le système de numération que nous utilisons couramment dans notre vie quotidienne. Il se compose de dix chiffres de base : 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9. Chaque chiffre a une valeur spécifique qui dépend de sa position dans un nombre.
Dans le système décimal, les nombres sont organisés en positions basées sur les puissances de dix. Pour mieux comprendre, prenons l'exemple du nombre 357. Chaque chiffre dans ce nombre a une valeur qui dépend de sa position : les centaines valent 300, les dizaines valent 50, et les unités valent 7.
Le système décimal fonctionne en incréments de dix. Lorsque nous atteignons la valeur 9 dans une position donnée, nous passons automatiquement à la position suivante et recommençons à compter à partir de zéro. Par exemple, si nous ajoutons 1 à 269, nous obtenons 270.
Un nombre entier se compose de différents rangs, tels que les unités, les dizaines, les centaines, etc. Chaque rang vaut dix fois le rang précédent, ce qui signifie qu'une centaine équivaut à dix dizaines, et une dizaine équivaut à 10 unités.
| Nombre = | Les milliers + | Les centaines + | Les dizaines + | Les unités + |
|---|---|---|---|---|
| Rang | 3 | 2 | 1 | 0 |
| Nombre = | 1 milliers + | 9 centaines + | 7 dizaines + | 6 unités |
| 1976 = | 1 x 103 | 9 x 102 | 7 x 101 | 6 x 100 |
| Valeur décimale = 1976 | 1000 | 900 | 70 | 6 |
1976 est décomposé en puissance de 10 et on peut décomposer n’importe quel nombre en puissance de sa base.
Ainsi, nous pouvons décomposer n'importe quel nombre en puissances de sa base, et un nombre est simplement la somme de ses différents rangs.
II. Le binaire
Le système binaire est un système de numération utilisé en informatique. À la différence du système décimal, qui utilise dix chiffres, le système binaire n'en utilise que deux : 0 et 1.
Le système binaire est utilisé en informatique car les ordinateurs utilisent des circuits électroniques qui peuvent être soit en position "éteinte" (0), soit en position "allumée" (1). Ces chiffres binaires sont ensuite utilisés pour représenter des informations numériques et des instructions.
Dans le système binaire, les nombres sont organisés en positions de puissances de deux. Chaque position a une valeur différente selon sa position.
Par exemple, le nombre 10011 occupe 5 bits. Chaque rang en binaire ne peut avoir que deux valeurs (binaire = base 2) différentes : 0 ou 1. Pour la base 10, chaque rang représente une puissance de 10, pour la base 2, chaque rang occupe une puissance de 2.
Voici comment compter en binaire jusqu'à 10 :
| Nombre en décimal | Nombre en binaire | Explication |
|---|---|---|
| 0 | 0 | 1er choix (rang 0) |
| 1 | 1 | 2ème choix (rang 0) |
| 2 | 10 | Le premier rang est complet, passons au suivant (rang 1) ! |
| 3 | 11 | On remplit à nouveau le rang 1. |
| 4 | 100 | Le rang 1 est plein, le rang 0 aussi, on passe au suivant (rang 2). |
| 5 | 101 | Nous continuons en suivant la même méthode. |
| 6 | 110 | |
| 7 | 111 | |
| 8 | 1000 | Nous commençons le rang 3. |
| 9 | 1001 | Nous continuons de la même manière qu'auparavant. |
| 10 | 1010 | |
| ... | ||
À retenir : Nous passons au rang suivant lorsque le rang actuel est complet.
Entraînement 1 :
Combien de valeurs peut-on coder avec 1 bit ?
Combien de valeurs peut-on coder avec 2 bits ?
Combien de valeurs peut-on coder avec 3 bits ?
Combien de valeurs peut-on coder avec n bits ?
III. Conversion d'un nombre décimal en binaire
Pour convertir un nombre décimal en binaire, nous utilisons une méthode appelée la "division par 2". Cette méthode consiste à effectuer une série de divisions par 2 jusqu'à ce que le quotient devienne égal à zéro. Ensuite, nous prenons tous les "restes" obtenus au fur et à mesure et les écrivons dans l'ordre inverse, du dernier au premier, pour obtenir la notation binaire.
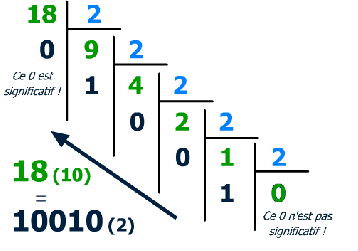
Entraînement 2 : Convertir un décimal en binaire
- Convertir (185)10 en base 2.
- Convertir (42)10 en base 2.
- Convertir (52)10 en base 2.
- Convertir (139)10 en base 2.
IV. Conversion d'un binaire en décimale
Pour convertir un nombre binaire en décimal, il faut associez à chaque chiffre binaire une valeur de position en fonction de sa position. La position la plus à gauche a une valeur de 2^0, la position suivante a une valeur de 2^1, la position suivante a une valeur de 2^2, et ainsi de suite. Chaque valeur de position est multipliée par le chiffre binaire correspondant. Le résultat est la somme de toutes les valeurs obtenues.
| Rang | 3 | 2 | 1 | 0 |
|---|---|---|---|---|
| binaire | 1 | 0 | 1 | 1 |
| Exposant = | 1 x 23 + | 0 x 22 + | 1 x 21 + | 1 x 20 |
| Valeur décimale = 11 | 8 + | 0 + | 2 + | 1 |
Entraînement 3 : Convertir du binaire en décimal
- Convertir (11010011)2 en base 10. Voir la solution
- Convertir (10011001)2 en base 10. Voir la solution
- Convertir (1111)2 en base 10. Voir la solution
- Convertir (101010)2 en base 10.
- Convertir (111000)2 en base 10.
V. L'hexadécimal
Le système hexadécimal est un système de numération qui utilise une base de 16. Il est largement utilisé en informatique et en programmation, car il offre une manière concise et pratique de représenter des données binaires.
Dans le système hexadécimal, nous utilisons les chiffres de 0 à 9 pour représenter les valeurs de 0 à 9, puis les lettres de A à F pour représenter les valeurs de 10 à 15. Voici la correspondance des chiffres hexadécimaux : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
| Binaire (base 2) | Décimal (base 10) | Hexadécimal (base 16) |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 10 | 2 | 2 |
| 11 | 3 | 3 |
| 100 | 4 | 4 |
| 101 | 5 | 5 |
| 110 | 6 | 6 |
| 111 | 7 | 7 |
| 1000 | 8 | 8 |
| 1001 | 9 | 9 |
| 1010 | 10 | A |
| 1011 | 11 | B |
| 1100 | 12 | C |
| 1101 | 13 | D |
| 1110 | 14 | E |
| 1111 | 15 | F |
Le chiffre le plus élevé en hexadécimal est F, correspondant à 15 en décimal et 1111 en binaire : F est donc encodé sur 4 bits (F)16 = 11112.
Pour convertir un nombre binaire en base 16, vous devez regrouper les bits par 4, ce qui vous donne un chiffre hexadécimal pour chaque groupe. Pour la conversion inverse, remplacez chaque chiffre hexadécimal par son équivalent binaire sur 4 bits.
Par exemple :
- (11011001)2 = (1101 1001)2 = D916
- 0x7F = (0111 1111)2 = (01111111)2
Entraînement 4 : Convertir du binaire en hexadécimal
- Convertir (101111011001)2 en base 16. Voir la solution
- Convertir (111011)2 en base 16. Voir la solution
- Convertir (101101)2 en base 16. Voir la solution
- Convertir (001100101)2 en base 16. Voir la solution
- Convertir (11110001)2 en base 16. (Exemple avec solution) Voir la solution
- Convertir (10011010)2 en base 16.
- Convertir (1101011)2 en base 16.
VI. Convertir un nombre décimal en hexadécimal
Pour convertir un nombre décimal en hexadécimal, la méthode est similaire au binaire, sauf que cette fois on divise par 16.
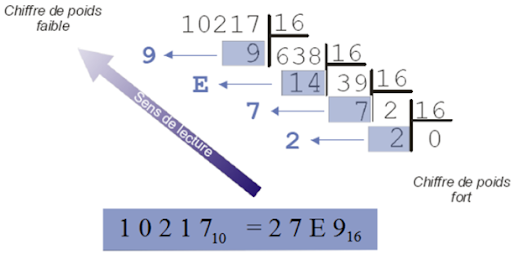
Entraînement 5 :
- Convertir (1387)10 en base 16
- Convertir (185)10 en hexadécimal Voir une solution
- Convertir (1024)10 en hexadécimal.
VII. Convertir un nombre hexadécimal en décimal
Pour convertir un nombre hexadécimal en décimal, le principe est similaire à la conversion "binaire en décimal", mais cette fois, nous utilisons des puissances de 16 au lieu de 2n.
Voici un exemple :
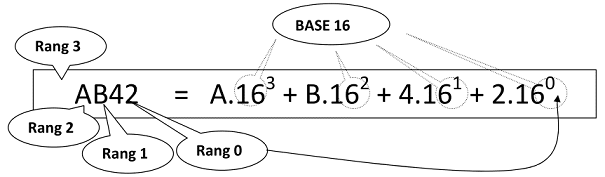
(AB42)16 = 10 x 163 + 11 x 162 + 4 x 161 + 2 x 160
(AB42)16 = 10 x 4096 + 11 x 256 + 4 x 16 + 2 x 1
(AB42)16 = 43842
Vous avez remarqué que lorsque nous rencontrons un chiffre en hexadécimal, nous le remplaçons par sa valeur décimale correspondante. Par exemple :
- un A est remplacé par un 10
- un B est remplacé par un 11
- un C est remplacé par un 12
- un D est remplacé par un 13
- un E est remplacé par un 14
- un F est remplacé par un 15
Entraînement 6 :
- Convertir (12B7)16 en base 10
- Convertir (4F3)16 en base 10
- Convertir (ABC)16 en base 10
VIII. Généralisation pour une base b
La conversion d'un nombre d'une base à une autre se fait en utilisant une méthode appelée la méthode de division successive.
La méthode de division successive consiste à diviser le nombre d'origine par la base cible jusqu'à ce que le quotient devienne zéro, en enregistrant les restes obtenus à chaque étape. Les restes, lus de bas en haut, forment le nombre converti dans la base cible.
Une solution en python :
def convertir (nombre, base):
"""base : entier au moins égal à 2 donné en base 10
nombre : entier naturel donné en base 10
renvoie l’écriture en base b d'un entier n par divisions en cascade"""
resultat = []
while nombre != 0:
resultat.append(nombre % base)
nombre = nombre // base
resultat.reverse()
return resultat
##################
print(convertir(15,2))Toutefois, lorsque b est supérieur ou égal à 10, de nouveaux symboles devront être introduits pour les restes obtenus supérieurs ou égaux à 10.
IX. Convertir avec python
# convertir dec -> bin
print("convertir dec -> bin : 125 : ",bin(125))
print("convertir dec -> bin : 78 : ",bin(78))
# convertir bin -> dec
print("convertir bin -> dec : 10101111 : ",0b10101111)
print("convertir bin -> dec : 10011001 : ",0b10011001)
# convertir dec -> hex
print("convertir dec -> hex : 257 : ",hex(257))
print("convertir dec -> hex : 161 : ",hex(161))
# convertir bin -> hex
print("convertir bin -> hex : 10101111 : ",hex(0b10101111))
print("convertir bin -> hex : 111001 : ",hex(0b111001))
# convertir hex -> dec
print("convertir hex -> dec : a3F : ",int(0xa3F))
print("convertir hex -> dec : 2ad : ",int(0x2ad))Savoir faire
- Savoir passer de la représentation d'une base dans une autre pour les bases 2,10,16
Fiche de cours