Les booléens
Numérique et sciences informatiques

Repères historiques
Georges BOOLE (1815-1864) était un mathématicien britannique qui a, entre autres, défini une représentation des opérations logiques à l’aide d’opérations mathématiques. On appelle cette modélisation l’algèbre de Boole et elle est à la base du fonctionnement des ordinateurs et plus généralement de tous les systèmes électroniques.

L'algèbre de Boole : Vrai ou Faux
L’algèbre de Boole est basée sur un ensemble de 2 valeurs, B = {0;1}, sur lequel on définit 3 opérations : ET, OU et NON. Leurs équivalents en anglais, les opérateurs and et or, sont couramment employés.
On appelle booléens les éléments de B.
Ces variables peuvent servir à constituer une information binaire (oui/non, vrai/faux, égal/différent, marche/arrêt, allumé/éteint , …) ou à décrire l'état physique d'un composant d'un système (alimentation d'un composant, action sur un bouton, ...)
La valeur 0 représente l’état physique d’un composant non alimenté, ou ne recevant pas d'action physique.
La valeur 1 représente l’état physique d’un composant alimenté.
A la base de tous les circuits actuels (sauf pour l’ordinateur quantique ...) se trouvent des composants nés de la physique quantique : les transistors. Vous pouvez-vous les représenter comme de minuscules interrupteurs. De nos jours, le transistor est tellement miniaturisé que votre ordinateur ou votre téléphone en contient plusieurs milliards sur une simple puce de silicium de la taille de votre ongle!
Les portes logiques
Les opérateurs booléens ont aussi en électronique des portes logiques qui se comportent de la même manière.
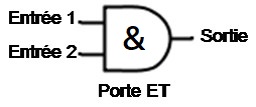
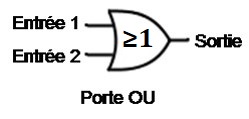
On définit ces opérations à l’aide des tableaux ci-dessous, qu’on appelle tables de vérité :
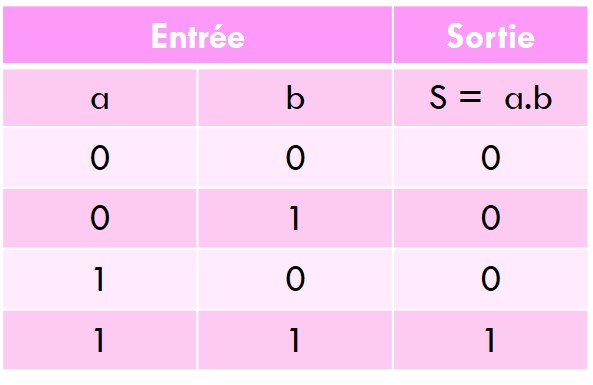
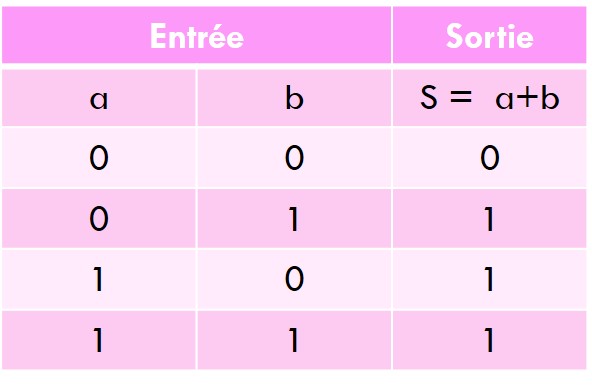
Ainsi, l’opérateur booléen and peut être considéré comme étant « les deux propositions sont vraie ».
L’opérateur booléen or quant à lui peut être interprété comme « au moins une des deux propositions est vraie ».
On remarque que a or b est vraie même si les deux sont vraie : on dit que le or est inclusif.
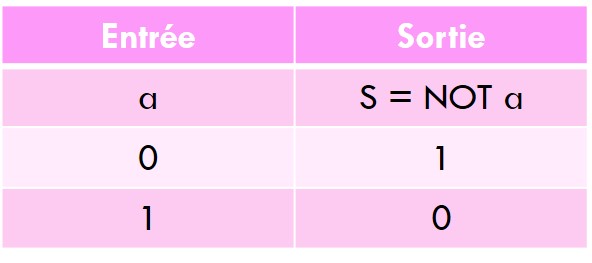
On définit également un opérateur not qui inverse la valeur de l’élément :
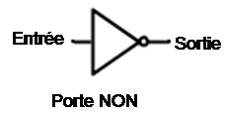
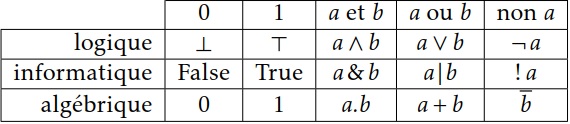
Il existe de nombreuses notations pour les opérateurs booléens ; dans la mesure où vous serez très certainement amenés à en rencontrer au hasard de la littérature sur le sujet, en voici quelques-unes des plus courantes :
Entraînement 1 :
Ouvrir le simulateur de circuits et créer pour chaque opération AND, OR, NOT un circuit électrique illustrant ses propriétés.
Propriétés fondamentales de l’algèbre de Boole
Éléments neutres :
- 0 est l'élément neutre de la fonction OU : \( a + 0 = a \)
- 0 est l'élément absorbant de la fonction ET : \( a \cdot 0 = 0 \)
- 1 est l'élément neutre de la fonction ET : \( a \cdot 1 = a \)
- 1 est l'élément absorbant de la fonction OU : \( a + 1 = 1 \)
Complémentarité :
- \( a + \overline{a} = 1 \)
- \( a \cdot \overline{a} = 0 \)
Commutativité :
- Produit logique : \( a \cdot b = b \cdot a \)
- Somme logique : \( a + b = b + a \)
Distributivité :
- Fonction ET par rapport à la fonction OU : \( a \cdot (b + c) = a \cdot b + a \cdot c \)
- Fonction OU par rapport à la fonction ET : \( a + (b \cdot c) = (a + b) \cdot (a + c) \)
Absorption :
- \( a + a \cdot b = a \cdot (1 + b) = a \)
Idempotence :
- \( a + a = a \)
- \( a \cdot a = a \)
Associativité :
- Produit logique : \( a \cdot (b \cdot c) = (a \cdot b) \cdot c = a \cdot b \cdot c \)
- Somme logique : \( a + (b + c) = (a + b) + c = a + b + c \)
Théorèmes de De Morgan :
- Premier théorème : \( \overline{a} + \overline{b} = \overline{a \cdot b} \)
- Deuxième théorème : \( \overline{a} \cdot \overline{b} = \overline{a + b} \)
Entraînement 2 :
Réaliser la table de vérité de A = a + b̅

Entraînement 3 :
Réaliser la table de vérité de B = (ā + b)*c
Entraînement 4 :
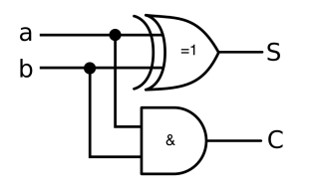
Additionner deux bits a et b avec la solution S en gardant la retenue C (care en anglais)
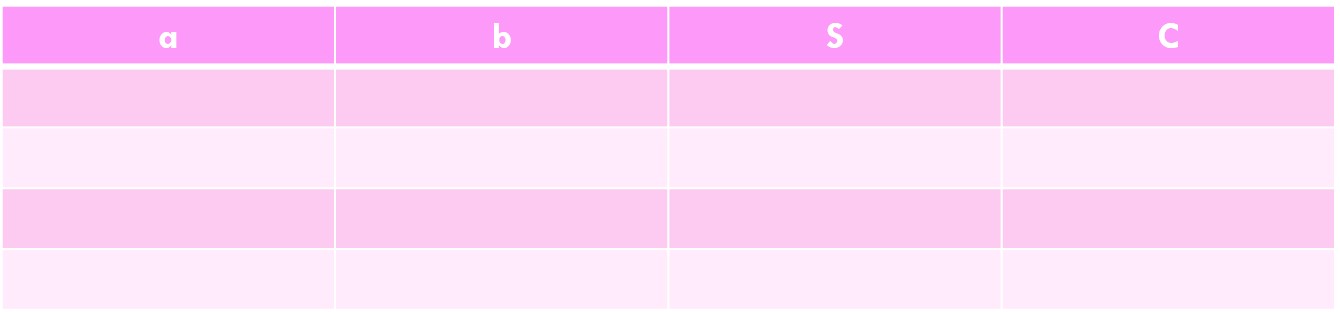
Entraînement 5 :
Démontrer l’égalité de la distributivité de la fonction ET par rapport à la fonction OU : a*(b + c) = a*b + a*c à l’aide des tables de vérité.

Entraînement 5 : Vérification de la distributivité
L’objectif est de démontrer l’égalité de la distributivité de la fonction ET par rapport à la fonction OU :
a AND (b OR c) = (a AND b) OR (a AND c), en remplissant une table de vérité.
Utilisez les valeurs possibles pour a, b et c et vérifiez que les deux expressions donnent les mêmes résultats.
Rappel des opérations logiques :
- ET (
AND) : DonneTrueuniquement si les deux valeurs sontTrue. - OU (
OR) : DonneTruesi au moins une des valeurs estTrue.
Table de vérité à compléter :
| a | b | c | b OR c | a AND (b OR c) | a AND b | a AND c | (a AND b) OR (a AND c) |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | |||||
| 0 | 0 | 1 | |||||
| 0 | 1 | 0 | |||||
| 0 | 1 | 1 | |||||
| 1 | 0 | 0 | |||||
| 1 | 0 | 1 | |||||
| 1 | 1 | 0 | |||||
| 1 | 1 | 1 |
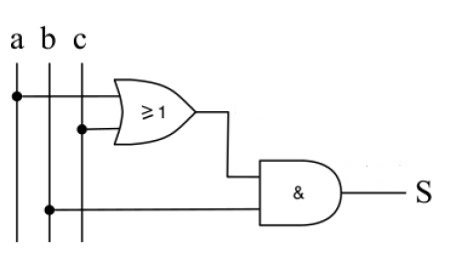
Entraînement 6 :
Donner le tableau de vérité et l’expression booléenne de ce circuit.
Entraînement 7 : Opérations logiques binaires
Effectuez les opérations logiques suivantes en binaire.Rappel :
-
& : ET logique (1 si les deux bits sont 1, sinon 0)
| : OU logique (1 si au moins un des bits est 1, sinon 0)
Exemple résolu :
1100 1101
& 1010 1010
----------
1000 1000
À vous de jouer :
1)
101 1011
& 101 0101
----------
2)
101 1011
| 101 0101
----------
3)
100 0011
| 101 0101
----------
Entraînement 8 : Trouver la Valeur de l'Expression
En utilisant l'ordre de priorité des opérations, calculez la valeur des expressions suivantes.
Consignes : Notez chaque étape intermédiaire pour simplifier les expressions et obtenez la valeur finale.
( ): Parenthèses (prioritaire)not: Négation logiqueand: ET logiqueor: OU logiquexor: OU exclusif (priorité la plus basse)
Exemple :
Expression :True or not False and FalseÉtapes :
- Évaluez
not False: True -
True and False: False - Évaluez
True or False: True
Résultat final : True
À vous de résoudre les expressions suivantes :
-
A =
True and (not False or True) xor (True and not False)
Résultat : _______
-
B =
(not False or False) and False xor (True and not False)
Résultat : _______
-
C =
(not False or True) and False or (False and not False)
Résultat : _______
Entraînement 9 :
Écrire dans le langage Python une fonction qui représente la table de vérité de la fonction logique ET. Plusieurs solutions sont possible.
Entraînement 11 :
Écrire dans le langage Python une fonction qui donne la table de vérité de OU.
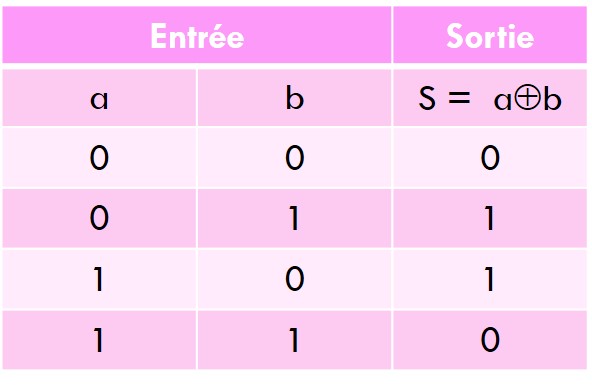
Entraînement 12 :
Écrire dans le langage Python une fonction qui donne la table de vérité de XOR le ou exclusif : (a and not b) or (not a and b), à l’aide des opérations usuelles sur les entiers..
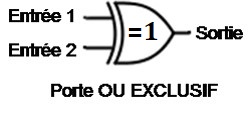
Remarques :Python et C++ évaluent les expressions logiques de manière paresseuses (on parle de lazy évaluation). Les opérateurs sont de type court-circuit :
OR n’évalue le deuxième argument que si le premier est faux.
AND n’évalue le deuxième argument si le premier est vrai.
Savoir faire
- Dresser la table d'une expression booléenne avec les opérateurs booléens : and, or, not et xor.
- Comprendre le caractère séquentiel de certains opérateurs booléens.
Fiche de cours