Algorithmes gloutons

Numérique et sciences informatiques

algorithme

Lors d'un trek en Basse Terre, vous tombez sur un gisement de pierres précieuses. A l'aide du web vous identifiez la valeur des pierres facilement.

Le problème du sac à dos : quelles boîtes choisir afin de maximiser la somme emportée tout en ne dépassant pas les 15 kg autorisés ?

sac à dos
Le problème du sac à dos :

Entraînement 1

Déterminez les objets que vous auriez intérêt à emporter, sachant que :

  • tous les objets devront tenir dans le sac à dos (15 Kg maxi)
  • vous cherchez à obtenir un gain maximum.

Ce genre de problème est un grand classique en informatique, on parle de problème d'optimisation . Il existe toujours plusieurs solutions possibles à un problème d'optimisation (dans le problème du sac à dos, on peut choisir A + E, D + C, B + E, ... Toutes les combinaisons sont possibles à partir du moment où la masse totale ne dépasse pas 15 Kg), mais on ne cherche pas n'importe quelle solution, on cherche une solution dite optimale : dans notre exemple on cherche le plus grand gain possible. Souvent, dans les problèmes d'optimisation, il n'existe pas une solution optimale, mais plusieurs solutions optimales, résoudre un problème d'optimisation c'est donc trouver une des solutions optimales .

Il existe différentes méthodes algorithmiques permettant de trouver une solution optimale à un problème d'optimisation : il peut, en effet, être intéressant "d'automatiser" la résolution des problèmes d'optimisation à l'aide d'algorithme (dans notre cas, trouver un algorithme qui trouve une solution optimale au problème du sac à doc).

En apparence, la solution la plus simple dans le cas du sac à dos serait d'écrire un algorithme qui teste toutes les combinaisons d'objets possibles et qui retient les solutions qui offrent un gain maximum. Dans notre cas précis, avec seulement 5 objets, cette solution pourrait être envisagée, mais avec un plus grand nombre d'objets, le temps de calculs, même pour un ordinateur très puissant, deviendrait trop important.
En effet l'algorithme qui testerait toutes les combinaisons possibles (on parle de force brute) aurait une complexité en temps en O(an) avec a une constante et n les nombre d'objets. On parle d'une complexité exponentielle. Les algorithmes à complexité exponentielle ne sont pas efficaces pour résoudre des problèmes, le temps de calcul devient beaucoup trop important quand n devient très grand.

À la place de cette méthode "je teste toutes les possibilités", il est possible d'utiliser une méthode dite gloutonne (greedy en anglais).

Qu'est-ce qu'une méthode gloutonne ?

La résolution d'un problème d'optimisation se fait généralement par étapes : à chaque étape on doit faire un choix. Par exemple, dans le problème du sac à dos, nous ajoutons les objets un par un, chaque ajout d'un objet constitue une étape: à chaque étape on doit choisir un objet à mettre dans le sac. Le principe de la méthode gloutonne est de, à chaque étape de la résolution du problème, faire le choix qui semble le plus pertinent sur le moment, avec l'espoir qu'au bout du compte, cela nous conduira vers une solution optimale du problème à résoudre. Autrement dit, on fait des choix localement optimaux dans l'espoir que ces choix mèneront à une solution globalement optimale (le "localement" signifie ici "à chaque étape de la résolution du problème").

Appliquons une méthode gloutonne à la résolution du problème du sac à dos :

  • Sachant que l'on cherche à maximiser le gain, commençons par établir un tableau nous donnant la "valeur massique" de chaque objet (pour chaque objet on divise sa valeur par sa masse) :

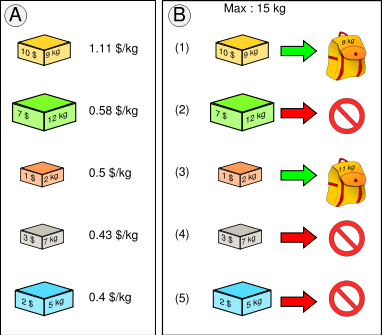
    sac à dos
    Optimisation du sac
    À gauche : tri des boîtes par ordre d'intérêt (ici en dollars par kilogramme). À droite : insertion dans l'ordre des boîtes, si cela est possible.
    valeur massique des objets
    objet A B C D E
    masse 12 Kg 9 Kg 7 Kg 5 Kg 2 Kg
    valeur marchande en k$ 7 10 3 2 1
    valeur massique 0,58 k$/Kg 1,11 k$/Kg 0,43 k$/Kg 0,4 k$/Kg 0,5 k$/Kg

  • On classe ensuite les objets par ordre décroissant de valeur massique : B(9kg) - A(12kg) -E(2kg) - C(7kg) - D(5kg)
  • Enfin, on remplit le sac en prenant les objets dans l'ordre et en s'arrêtant dès que la masse limite est atteinte. C'est ici que ce fait "le choix glouton", à chaque étape, on prend l'objet ayant le rapport "valeur-masse" le plus intéressant au vu des objectifs :
    • 1re étape : B (9 Kg)
    • 2e étape : B + A (9+ 12 = 21 Kg) => impossible, on dépasse les 15 Kg.
    • 3e étape : B + E (9+ 2 = 11 Kg)
    • 4e étape : B + E + C > 15 kg => impossible, on dépasse les 15 Kg.
    • 5e étape : B + E + D > 15 kg => impossible, on dépasse les 15 Kg.

On obtient ici une solution de 11 $ pour 11 kg.

Cette méthode gloutonne peut être "automatisée", il est donc possible d'écrire un algorithme glouton (un algorithme qui est basé sur une méthode gloutonne) afin de trouver une solution au problème du sac à dos avec n'importe quelles valeurs (nombre d'objets, masse des objets, valeur des objets, masse maximum).

La solution trouvée ci-dessus est-elle optimale ?

On constate rapidement que la réponse est non, car la solution optimale est de 12 $ et 14 kg. Dans notre problème, la méthode gloutonne ne nous donne pas une solution optimale.

Plus généralement , il est important de bien comprendre qu'un algorithme glouton ne donne pas forcement une solution optimale.

Examinons un autre problème d'optimisation : le problème du rendu de monnaie

Nous sommes des commerçants, nous devons rendre la monnaie à un client.

Ce problème est un grand classique de l'algorithmique.

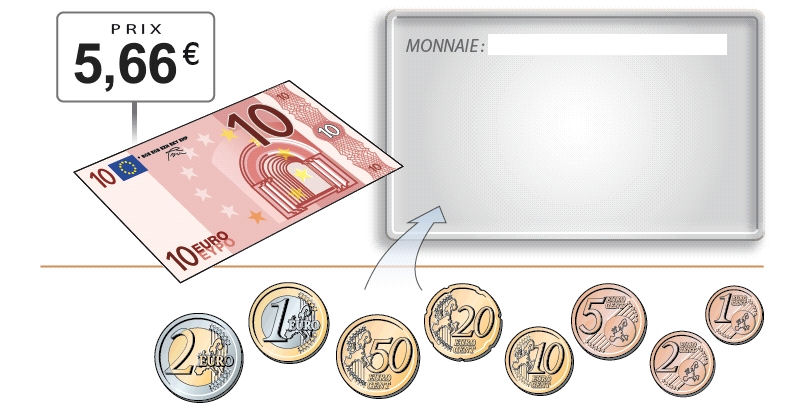
sac à dos
Rendu de monaie

Supposons qu'on doive vous rendre la somme de 4.34€ (10 - 5.66).

Il y a plusieurs façons de procéder. On peut par exemple vous rendre 434 pièces de 1 cent ou 43 pièces de 10 cents et 4 pièces de 1 cents.

Il y a bien évidemment énormément de possibilités.

Il y a fort à parier que les solutions du type "434 pièces de 1 cent" ne vous conviennent pas, pour cause, personne n'a envie de remplir son porte monnaie avec autant de pièces...

Le problème qui se pose est donc de minimiser le nombre de pièces rendues pour un montant fixé.

Solution naïve

La solution a laquelle on pense immédiatement est d'énumérer toutes les combinaisons possibles, de sélectionner celles qui impliquent un minimum de pièces et de choisir la meilleure.

Cette solution, dite de force brute, fonctionnera toujours mais est très loin d'être efficace car elle implique en général un nombre très important de combinaisons différentes, ce qui nuit grandement à l'efficacité de notre solution.

Notre tâche va donc être de formuler une solution plus efficace pour ce type de problème.

La méthode gloutonne

La méthode gloutonne vise donc à optimiser la résolution d'un problème en partant du principe suivant :

Des choix locaux optimaux, étape après étape, devraient produire un résultat global optimal.

Dans notre cas, on va répéter le choix de la pièce de plus grande valeur qui ne dépasse pas la somme restante.

Prenons un exemple concret, celui que nous avons introduit précédemment.
On doit donc nous rendre la somme de 4.34€ et on dispose du système de monnaie européen, à savoir ceci :
PIÈCES (en cents) : [1,2,5,10,20,50,100,200]

Appliquons donc la méthode gloutonne pour voir le choix à faire dans ce cas ci. 
ÉTAPE 1 :
 - Somme à rendre : 434 cents
 - Solution locale : 200
 - Pièces utilisées : 1*2€

ÉTAPE 2 :
 - Somme à rendre : 234 cents
 - Solution locale : 200
 - Pièces utilisées : 2*2€

ÉTAPE 3 :
 - Somme à rendre : 34 cents
 - Solution locale : 20
 - Pièces utilisées : 2 * 2€ + 1 * 20 cents

ÉTAPE 4 :
 - Somme à rendre : 14 cents.
 - Solution locale : 10
 - Pièces utilisées : 2 * 2€ + 1 * 20 cents + 1 * 10 cents

ÉTAPE 5 :
 - Somme à rendre : 4 cents
 - Solution locale : 2
 - Pièces utilisées : 2 * 2€ + 1 * 20c ents + 1 * 10 cents + 1 * 2 cents 

ÉTAPE 5 :
 - Somme à rendre : 2 cents
 - Solution locale : 2
 - Pièces utilisées : 2 * 2€ + 1 * 20 cents + 1 * 10 cents + 2 * 2 cents 
On a rendu toute la monnaie, on s'arrête là !
L'algorithme

On va récupérer les données sous forme d'une liste (pour le système monétaire en vigueur) et d'un entier (pour le rendu).

De là :

  • Tant que le rendu est supérieur à la pièce de plus haute valeur (située en première position dans la liste) on retranchera la valeur de cette pièce au rendu et on ajoutera la pièce dans une liste qui constituera la solution.
  • Si le rendu est inférieur à la pièce de plus haute valeur en cours, on passe à la pièce suivante.
  • Et ce jusqu'à ce que le rendu soit nul
Puis rajoutez ce qu'il faut pour que ce soit l'utilisateur qui rentre la somme à rendre

Entraînement 2

À partir de la méthode gloutonne, élaborée ci-dessus, complétez la fonction rendu_monnaie(somme_due, somme_versee) en python qui permettra de déterminer le nombre minimal de pièces à utiliser pour une somme donnée. La fonction rendu_monnaie prend en paramètres deux nombres entiers positifs somme_due et somme_versee. Elle procède au rendu de la monnaie de la différence somme_versee – somme_due pour des achats effectués avec le système monétaire de la zone Euro. On utilise pour cela un algorithme glouton qui commence par rendre le maximum de pièces ou billets de plus grandes valeurs et ainsi de suite. Par la suite, on assimilera les billets à des pièces.

La fonction rendu_monnaie renvoie un tableau de type list contenant les pièces qui composent le rendu. Toutes les sommes sont exprimées en euros. Les valeurs possibles pour les pièces sont donc contenues dans le tableau pieces = [1, 2, 5, 10, 20, 50, 100, 200].

Ainsi, l’instruction rendu_monnaie(452, 500) renvoie le tableau [20,20,5,2,1]. En effet, la somme à rendre est de 48 euros soit 20 + 20 + 5 + 2 + 1 

# Liste des valeurs des pièces disponibles
pieces = [1, 2, 5, 10, 20, 50, 100, 200]

def rendu_monnaie(somme_due, somme_versee):
    """
    Fonction pour calculer la monnaie à rendre en utilisant les pièces disponibles.
    Args:
        somme_due (int): La somme à rendre.
        somme_versee (int): La somme effectivement versée.
    Returns:
        list: Liste des pièces à rendre.
    """
    # Initialisation de la liste des pièces à rendre
    rendu = ...
    # Calcul du montant restant à rendre
    a_rendre = ...
    # Initialisation de l'index pour parcourir les pièces de la plus grande à la plus petite
    i = len(pieces) - 1
    # Tant qu'il reste de l'argent à rendre
    while ... :
        # Vérifier si la pièce actuelle est inférieure ou égale au montant à rendre
        if pieces[i] <= a_rendre:
            # Ajouter la pièce à la liste des pièces rendues
            rendu.append(...)
            # Soustraire la valeur de la pièce du montant à rendre
            a_rendre -= ...
        else:
            # Passer à la pièce de valeur inférieure
            i -= ...
    # Retourner la liste des pièces à rendre
    return rendu

# Assertions pour tester la fonction rendu_monnaie avec différents cas
# Cas où la somme due est égale à la somme versée, aucun rendu n'est nécessaire
assert rendu_monnaie(100, 100) == [], "Cas où aucune pièce n'est nécessaire"
# Cas où la somme due est inférieure à la somme versée et nécessite un rendu
assert rendu_monnaie(123, 200) == [50, 20, 5, 2], "Cas où un rendu de monnaie est nécessaire"

print("Tous les tests ont réussi !")

Fiche de cours