Informatique au lycée Faustin Fleret

La notion d' algorithme est souvent associée à l'informatique, pourtant le terme algorithme vient du nom du mathématicien perse du 9e siècle Muhammad Ibn Mūsā al-Khuwārizmī. La notion d'algorithme est donc très antérieure à la création du premier ordinateur.

Mais qu'est-ce qu'un algorithme ?

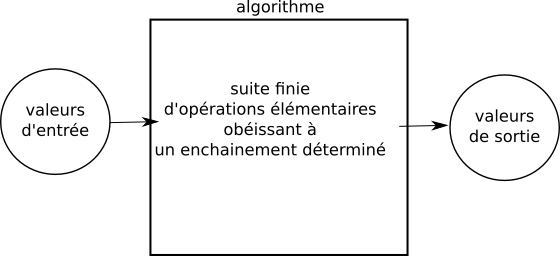
Pour résoudre un problème, réaliser une tâche, un ordinateur doit effectuer une succession d’instructions : la solution est appelée algorithme.
Nous dirons que c’est un ensemble de règles permettant de résoudre un problème sur des données d’entrée. Cet ensemble de règle définit avec précision un ensemble de séquences d’instructions qui se terminent en un temps fini.

On pourrait résumer ce qu'est un algorithme par le schéma suivant :

Dans un premier temps rédiger un algorithme consiste à décrire les différentes étapes de calcul pour résoudre un problème algébrique, numérique ou décisionnel.

Exemple :

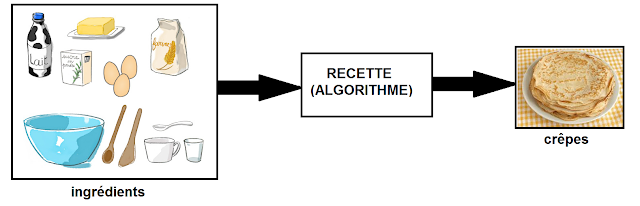
Une recette de cuisine, par exemple, est un algorithme : une suite d'opérations simples permettant de passer des ingrédients à un plat préparé.

On représente souvent l'algorithme de façon schématique, en décomposant les étapes et en les reliant par des flèches, un peu comme ci-dessous :

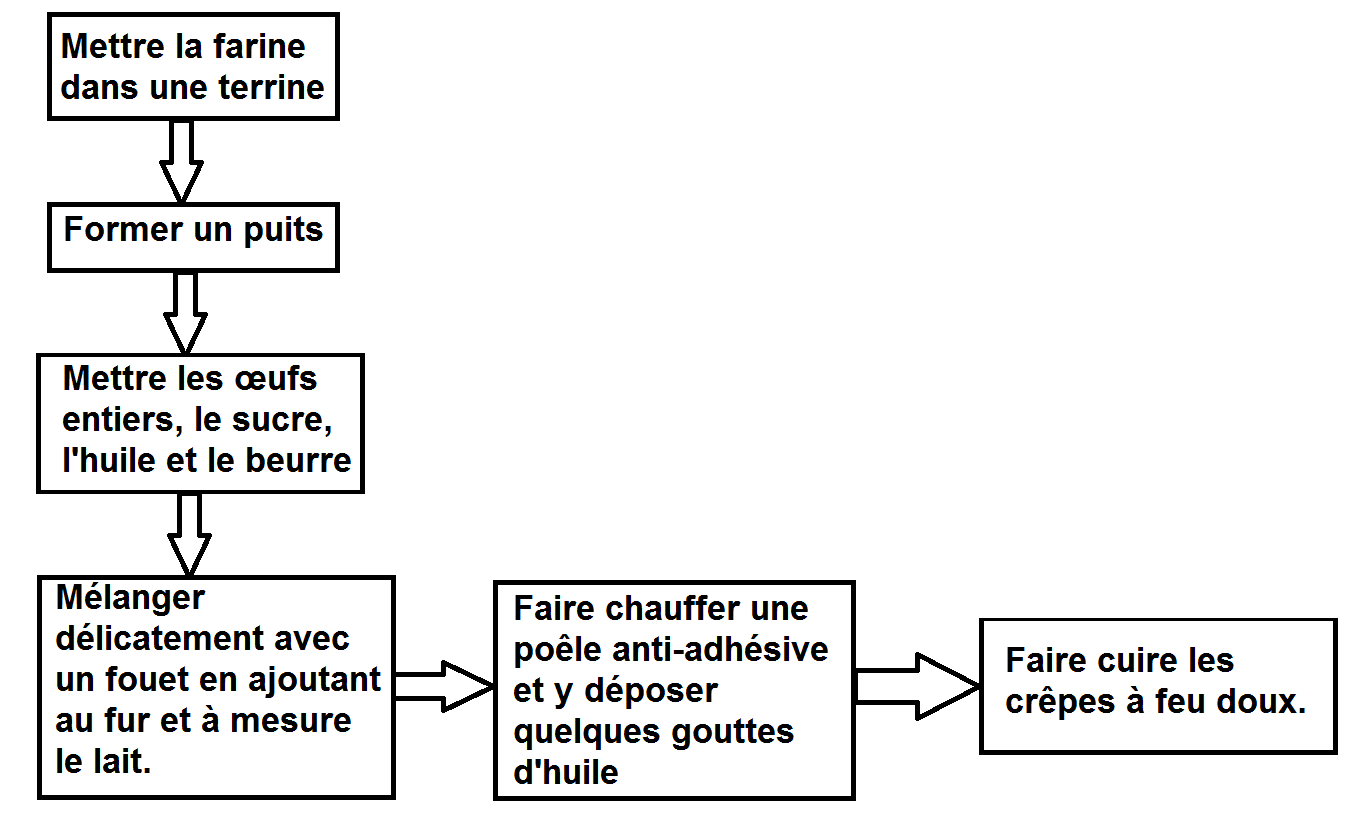
Pour faire des crêpes, il suffit de suivre les instructions dans l'ordre. Les recettes sont des algorithmes destinés aux humains et sont donc écrites dans un langage compréhensible par des humains. Comme on suppose que les humains sont raisonnablement intelligents, il y a plein de choses qu'on n'a pas besoin de préciser dans la recette, par exemple qu' il faut retirer la coquille des œufs ou ne pas utiliser du lait de raton-laveur.
En plus, l'algorithme de la recette des crêpes est très simple car il n'y a qu'un seul choix possible à chaque étape. Pour aborder cette notion de choix, nous allons considérer un autre algorithme : celui qui permet de déterminer si on peut faire des crêpes ou non, en fonction de ce qu'il y a dans le frigo et les placards.

Les conditions dans les algorithmes

Avant de se lancer dans la confection des crêpes, on vérifie d'ordinaire qu'on a bien tout ce qu'il faut. Pour s'assurer qu'on dispose de suffisamment d'ingrédients, voici un des algorithmes qu'on pourrait utiliser, sachant qu'il faudra des œufs, du lait, de la farine, du sucre et du beurre. Dans ce schéma, on va vérifier une à une toutes les conditions nécessaires au bon déroulement de la préparation des crêpes.

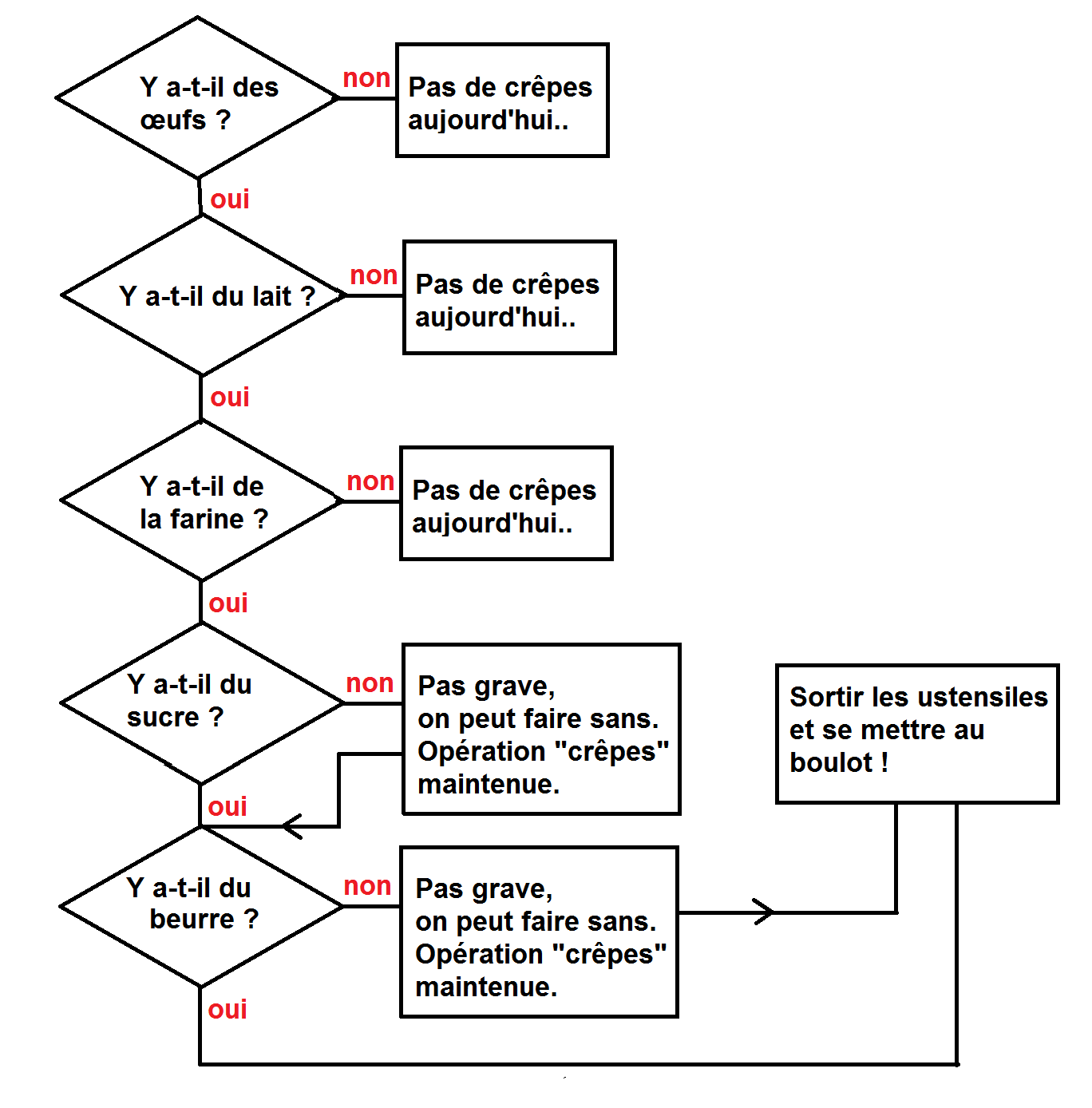
De manière générale, un algorithme sert à traiter ce qu'on appelle des "entrées" (dans notre cas, les ingrédients et le matériel de cuisine) pour donner un résultat (les crêpes). Les instructions décrites dans l'algorithme doivent être très simples et ne pas porter à confusion. Pour obtenir le même résultat, il existe une infinité d'algorithmes possibles. Dans la recette des crêpes, on pourrait rajouter une étape consistant à faire tourner la bouteille de lait cinq fois sur elle même avant de s'en servir. Cela ne changerait rien au résultat : c'est donc une étape inutile. Un bon algorithme est une recette facile à suivre, qui ne fait pas perdre de temps inutilement et qui ne provoque pas d'erreurs. Un bon algorithme doit aussi avoir un début et surtout .. une fin ! Tous les informaticiens du monde se sont un jour retrouvés confrontés à l'horreur absolue d'une boucle infinie, condamnés à faire des crêpes ad vitam æternam.

Tout algorithme est donc caractérisé par :

• Un ensemble d’instructions à exécuter
• Un ordre d’exécution de ces différentes actions, déterminé par la logique d’enchaînement et conditionné par les structures mises en œuvre.
• un début et une fin

Trois phases indissociables structurent un algorithme :

1. La préparation du traitement
2. Le traitement de donnée(s)
3. La sortie de résultat(s)

Exemple :

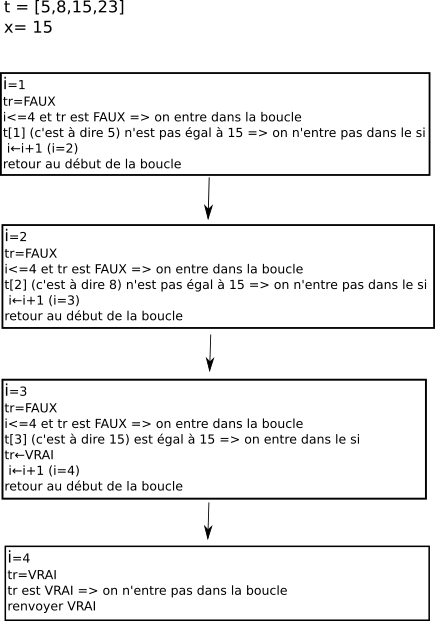
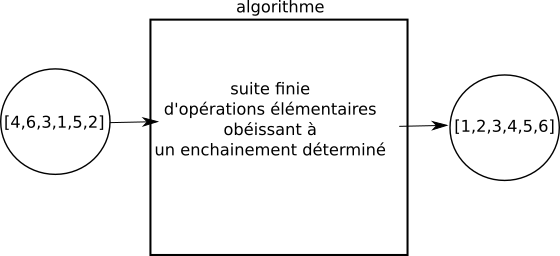
Nous allons étudier cette année, ainsi que l'année prochaine, des algorithmes de tri pour les tableaux (un tableau ressemble beaucoup à une liste en Python, même si ce n'est pas exactement la même chose). Nous avons en entrée un tableau non trié et nous obtenons en sortie un tableau trié :

La "valeur de sortie" n'est pas obligatoirement du même type que la "valeur d'entrée". Prenons l'exemple d'un algorithme qui prend en entrée un tableau t d'entiers et un entier x, et qui "répond" par "oui" ou par "non" à la question "x est-il présent dans le tableau t ?". Dans ce cas, la "valeur de sortie" sera "oui" ou "non".

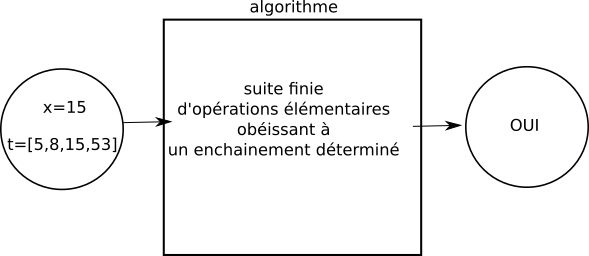
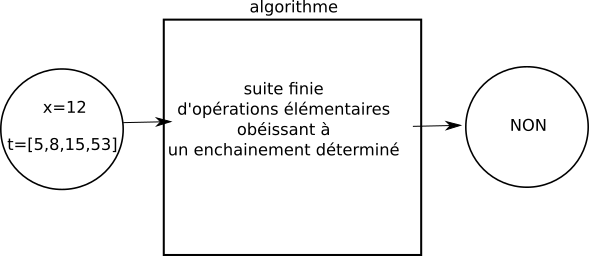
Essayons d'écrire l'algorithme décrit ci-dessus :

Nous devons trouver la suite d'opérations élémentaires qui permettra de répondre à la question : "x est-il présent dans le tableau t ?"

VARIABLE
	t : tableau d'entiers
	x : nombre entier
	tr : booléen (VRAI ou FAUX)
	i : nombre entier (pour l'itération)
DEBUT
	tr ← FAUX
	i ← 1
	TantQue i <= longueur(t) Et que tr == FAUX:
		  Si t[i] == x:
			tr ← VRAI
		  FinSi
		  i ← i + 1
	Fin TantQue
	Renvoyer la valeur de tr
FIN