Représentation binaire d'un entier relatif

Numérique et sciences informatiques

donnees

I. Les opérations en binaire : addition et multiplication

L'addition en binaire

En binaire (0,1), les règles d'addition sont simples :

1 + 0 = 1
0 + 1 = 1
0 + 0 = 0
1 + 1 = 10 (0 avec une retenue de 1)

Exemple :

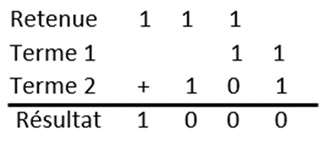
addition en binaire
Exemple d'addition en binaire

La multiplication en binaire

En binaire (0,1), les règles de multiplication sont également simples :

1 * 0 = 0
0 * 0 = 0
1 * 1 = 1
0 * 1 = 0

Exemple :

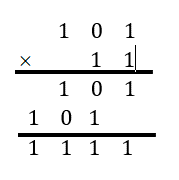
multiplication en binaire
Exemple de multiplication en binaire

Entraînement 1 :

  1. Calculez la somme de (1001 1101)2 et (0001 1111)2.

    2. Voir une solution

  2. Réalisez la somme de (1101 1101)2 et (0001 1111)2.

    3. Voir une solution

  3. Calculez le produit de (1101)2 et (1111)2.

    4. Voir une solution

  4. Réalisez la somme de (10101)2 et (1101)2.
  5. Calculez le produit de (101)2 et (100)2.

II. Convertir un entier négatif en binaire

1ère méthode : Le complément à 2

Pour convertir un entier négatif en binaire, nous utilisons la méthode du complément à deux.

Avant de représenter un entier relatif, il est nécessaire de définir le nombre de bits qui seront utilisés pour cette représentation (souvent 8, 16, 32 ou 64 bits).

Prenons un exemple : déterminons la représentation de -12 sur 8 bits.

  1. Commençons par représenter 12 sur 8 bits (sachant que pour représenter 12 en binaire seuls 4 bits sont nécessaires, les 4 bits les plus à gauche seront à 0) : (12)10 = (00001100)2
  2. Inversons tous les bits (les bits à 1 passent à 0 et vice versa) : 11110011
  3. Ajoutons 1 au nombre obtenu à l'étape précédente :
    Ajout de 1 avec retenues marquées en rouge
  4. Le résultat de l'opération représente -12 sur 8 bits : (-12)10 = (11110100)2

Vérification :

Pour vérifier, nous pouvons réaliser l'opération 12 + (-12) et constater que le résultat est zéro.

Vérification avec représentation graphique

Dans l'opération ci-dessus, nous avons un 1 pour le 9e bit, mais comme notre représentation se limite à 8 bits, il nous reste bien 00000000.

Entraînement 2 :

En utilisant le complément à 2, représentez -15 (représentation sur 8 bits)

Il faut noter que si le bit de poids fort est à 1, l'entier est négatif, si le bit de poids fort est à 0, il est positif.

2ème méthode :

Il existe une autre méthode pour trouver le complément à deux sans faire de calcul :

  1. Noter la représentation binaire de l'entier positif
  2. En partant de l'unité (de la droite), on recopie jusqu'au premier bit égal à 1 inclus.
  3. On inverse tous les autres.

Exemple 1 : combien vaut -9 en binaire ?
(9)10 =(00001001)2
00001001 en rouge la partie à inverser
(-9)10 = (11110111)2

Exemple 2 : combien vaut -8 en binaire ?
(8)10 = (00001000)2
00001000 en rouge la partie à inverser
(-8)10 = (11111000)2



Entraînement 3 :

Représentez sur 8 bits l'entier 4 puis représentez, toujours sur 8 bits, l'entier -5. Additionnez ces 2 nombres (en utilisant les représentations binaires bien évidemment), vérifiez que vous obtenez bien -1.


Entraînement 4 : Représentation d'entiers négatifs sur 8 bits

Question 1 :
  1. Représentez -5 en utilisant le complément à deux sur 8 bits.
    2. Voir la solution
Question 2 :
  1. Quelle est la représentation binaire de -64 sur 8 bits en utilisant le complément à deux ?
    2. Voir la solution
Question 3 :
  1. Représentez -127 sur 8 bits en utilisant le complément à deux.
    2. Voir la solution

Entraînement 5 :

  1. Quel est le plus petit entier négatif que l'on peut représenter sur 8 bits avec le complément à 2 ?
    2. Voir une solution

  2. Quel est le plus grand entier positif avec le complément à 2 que l'on peut représenter sur 8 bits ?
    3. Voir une solution

  3. Quelles sont les bornes inférieure et supérieure d'un entier relatif codé sur 16 bits ?
    4. Voir une solution



Savoir faire

  • Évaluer le nombre de bits nécessaires à l'écriture en base 2 d'un entier, de la somme ou du produit de deux nombres entiers.
  • Utiliser le complément à 2.

Fiche de cours