Informatique au lycée Faustin Fleret

L'algorithme des k plus proches voisins (k-NN) (en anglais "k nearest neighbors" : knn) est une technique de classification supervisée. Elle est utilisée pour classer les objets en fonction de leurs caractéristiques en comparant les objets à ceux qui leur ressemblent le plus.

L'idée de base de l'algorithme est de trouver les k objets les plus proches de l'objet à classer et de déterminer la classe de l'objet à partir de la classe majoritaire parmi ces k voisins.

Principe de K-NN : dis moi qui sont tes voisins, je te dirais qui tu es !

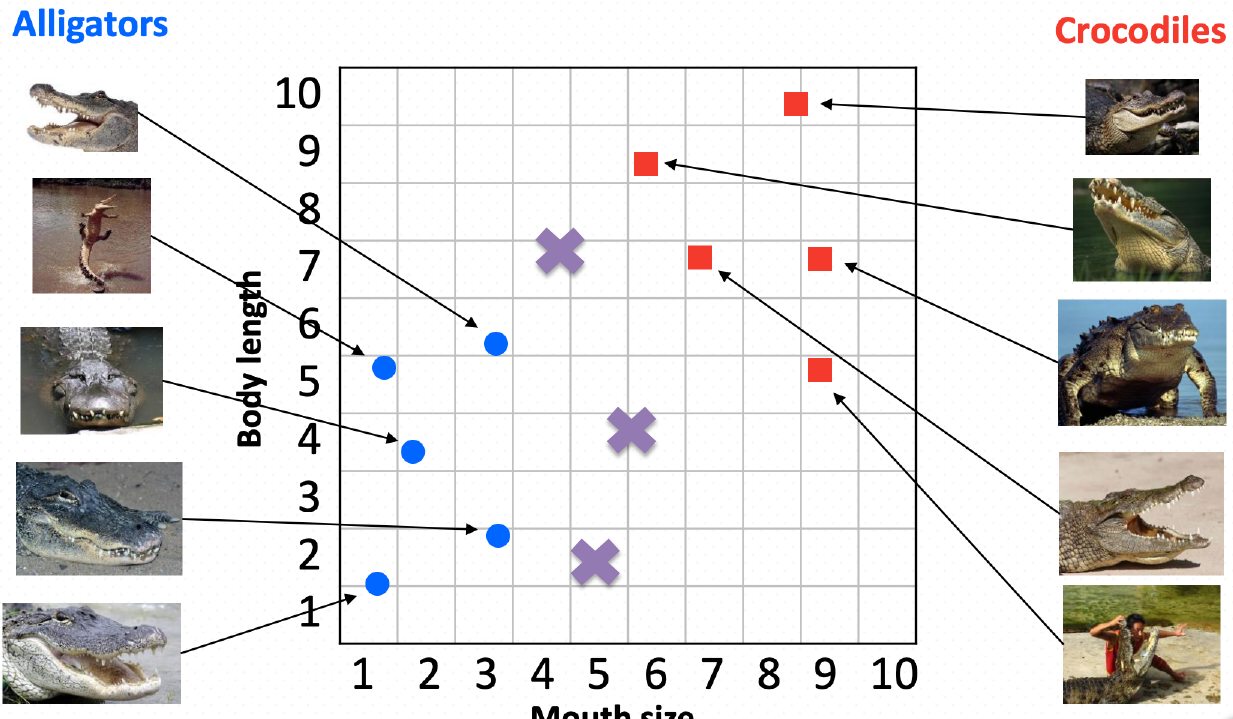
La classification permet de prédire si un élément est membre d’un groupe ou d’une catégorie donnée. A partir de cas, la méthode permet de prendre des décisions en recherchant un ou des cas similaires déjà résolus.

L'algorithme KNN est utilisé dans divers domaines tels que la reconnaissance de caractères manuscrits, la reconnaissance vocale, la détection de spam et la recommandation de produits, la détection de pathologies. Par exemple, il peut être utilisé pour recommander des films à un utilisateur en fonction des films qu’il a déjà regardés et aimés ou prédire si un patient est atteint d’une maladie cardiaque ou non en fonction de ses antécédents médicaux.

Principe de l'algorithme des k plus proches voisins

L'algorithme des k plus proches voisins (k-NN) est une méthode d'apprentissage supervisé utilisée pour la classification ou la régression. Le principe de base est de trouver les k exemples les plus similaires à un exemple donné dans un ensemble de données, puis de prédire la classe ou la valeur cible de l'exemple à partir des classes ou des valeurs des exemples les plus proches.

Plus précisément, voici les étapes de l'algorithme des k plus proches voisins :

1. Calculer la distance entre l'exemple à classer et tous les autres exemples de l'ensemble de données. La distance la plus couramment utilisée est la distance euclidienne, mais d'autres distances peuvent être utilisées en fonction du problème spécifique.
2. Sélectionner les k exemples les plus proches de l'exemple à classer en fonction de leur distance.
3. Si l'algorithme est utilisé pour la classification, la classe majoritaire des k exemples est attribuée à l'exemple à classer. Si l'algorithme est utilisé pour la régression, la valeur moyenne des k exemples est attribuée à l'exemple à classer.

Exemple de classification avec k-NN

Pour mieux comprendre le fonctionnement de l'algorithme des k plus proches voisins, nous allons utiliser un exemple de classification. Nous allons utiliser le célèbre ensemble de données Iris, qui contient des mesures de différentes espèces d'iris. Nous allons utiliser k-NN pour prédire la classe de chaque iris en fonction de ses mesures.

En 1936, Edgar Anderson a collecté des données sur 3 espèces d'iris : "iris setosa", "iris virginica" et "iris versicolor"

Pour chaque iris étudié, Edgar Anderson a mesuré (en cm) :

• la largeur des sépales
• la longueur des sépales
• la largeur des pétales
• la longueur des pétales

Par souci simplification, nous nous intéresserons uniquement à la largeur et à la longueur des pétales.

Pour chaque iris mesuré, Anderson a aussi noté l'espèce ("iris setosa", "iris virginica" ou "iris versicolor")

Vous trouverez 50 de ces mesures dans le fichier iris.csv

En résumé, vous trouverez dans ce fichier :

• la longueur des pétales
• la largeur des pétales
• l'espèce de l'iris (au lieu d'utiliser les noms des espèces, on utilisera des chiffres : 0 pour "iris setosa", 1 pour "iris virginica" et 2 pour "iris versicolor")

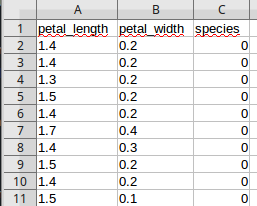
Avant d'entrer dans le vif du sujet (algorithme knn), nous allons chercher à obtenir une représentation graphique des données contenues dans le fichier iris.csv

import pandas
import matplotlib.pyplot as plt
iris = pandas.read_csv("iris.csv")  # lecture du fichier iris.csv 

x = iris.loc[:,"petal_length"]  # abscisse : longueur de la pétale, 
y = iris.loc[:,"petal_width"]  # ordonnée : largeur de la pétale
lab = iris.loc[:,"species"]

plt.scatter(x[lab == 0], y[lab == 0], color='g', label='setosa')
plt.scatter(x[lab == 1], y[lab == 1], color='r', label='virginica')
plt.scatter(x[lab == 2], y[lab == 2], color='b', label='versicolor')
plt.legend()
plt.show()  # affiche le graphique 

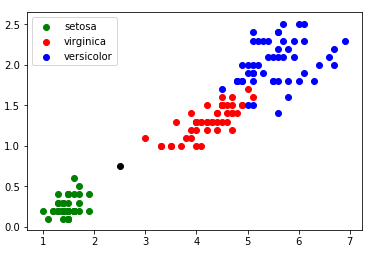
Vous devriez normalement obtenir ceci :

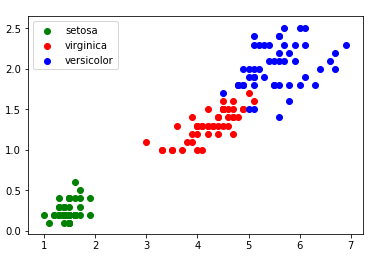
Nous obtenons des "nuages" de points, on remarque ces points sont regroupés par espèces d'iris (sauf pour "iris virginica" et "iris versicolor", les points ont un peu tendance à se mélanger).

Imaginez maintenant qu'au cours d'une promenade vous trouviez un iris, n'étant pas un spécialiste, il ne vous est pas vraiment possible de déterminer l'espèce. En revanche, vous êtes capables de mesurer la longueur et la largeur des pétales de cet iris. Partons du principe qu'un pétale fasse 0,5 cm de large et 2 cm de long. Plaçons cette nouvelle donnée sur notre graphique (il nous suffit d'ajouter la ligne "plt.scatter(2.0, 0.5, color='k')", le nouveau point va apparaître en noir (color='k')) :

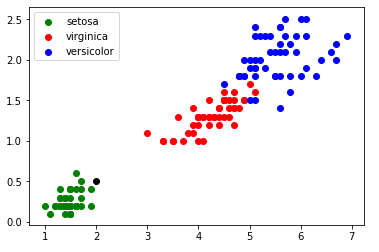
Je pense que le résultat est sans appel : il y a de fortes chances que votre iris soit de l'espèce "iris setosa".

Il est possible de rencontrer des cas plus difficiles, par exemple : largeur du pétale = 0,75 cm ; longueur du pétale = 2,5 cm :

Dans ce genre de cas, il peut être intéressant d'utiliser l'algorithme des "k plus proches voisins", en quoi consiste cet algorithme :

• on calcule la distance entre notre point (largeur du pétale = 0,75 cm ; longueur du pétale = 2,5 cm) et chaque point issu du jeu de données "iris" (à chaque fois c'est un calcul de distance entre 2 points tout ce qu'il y a de plus classique)
• on sélectionne uniquement les k distances les plus petites (les k plus proches voisins)
• parmi les k plus proches voisins, on détermine quelle est l'espèce majoritaire. On associe à notre "iris mystère" cette "espèce majoritaire parmi les k plus proches voisins"

Prennons k = 3

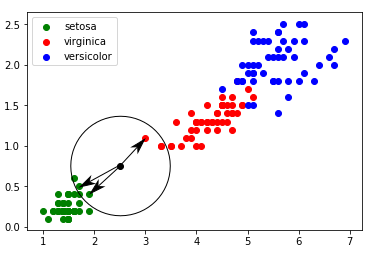
Les 3 plus proches voisins sont signalés ci-dessus avec des flèches : nous avons deux "iris setosa" (point vert) et un "iris virginica" (point rouge). D'après l'algorithme des "k plus proches voisins", notre "iris mystère" appartient à l'espèce "setosa".

La bibliothèque Python Scikit Learn propose un grand nombre d'algorithmes lié au machine learning (c'est sans aucun doute la bibliothèque la plus utilisée en machine learning). Parmi tous ces algorithmes, Scikit Learn propose l'algorithme des k plus proches voisins.

import pandas
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier

#traitement CSV
iris = pandas.read_csv("iris.csv")
x = iris.loc[:,"petal_length"]
y = iris.loc[:,"petal_width"]
lab = iris.loc[:,"species"]

#valeurs
longueur = 2.5
largeur = 0.75
k=3

#graphique
plt.scatter(x[lab == 0], y[lab == 0], color = 'g', label = 'setosa')
plt.scatter(x[lab == 1], y[lab == 1], color = 'r', label = 'virginica')
plt.scatter(x[lab == 2], y[lab == 2], color = 'b', label = 'versicolor')
plt.scatter(longueur, largeur, color='k')
plt.legend()

#algo knn
d = list(zip(x,y))
model = KNeighborsClassifier(n_neighbors = k)
model.fit(d,lab)
prediction = model.predict([[longueur,largeur]])

#Affichage résultats
txt = "Résultat : "
if prediction[0] == 0:
  txt = txt+"setosa"
if prediction[0] == 1:
  txt = txt+"virginica"
if prediction[0] == 2:
  txt = txt+"versicolor"
plt.text(3,0.5, f"largeur : {largeur} cm longueur : {longueur} cm", fontsize = 12)
plt.text(3,0.3, f"k : {k}", fontsize = 12)
plt.text(3,0.1, txt, fontsize = 12)

plt.show()
			

Le code effectue la classification des fleurs d'iris en utilisant l'algorithme des k plus proches voisins (kNN) :

1. Copier le code

   d = list(zip(x,y))

   : Cette ligne crée une liste de tuples en utilisant la fonction zip qui combine les données de longueur des pétales x et de largeur des pétales y des fleurs d'iris en un seul tuple. La fonction list est utilisée pour convertir l'objet zip en une liste.
2. Copier le code

   model = KNeighborsClassifier(n_neighbors = k)

   : Cette ligne crée un objet de modèle d'instance KNeighborsClassifier de la bibliothèque sklearn.neighbors pour implémenter l'algorithme k-NN. Le nombre de voisins à considérer k est spécifié en tant qu'argument n_neighbors.
3. Copier le code

   model.fit(d,lab)

   : Cette ligne entraîne le modèle en utilisant les données d'entraînement d (qui contiennent les mesures de longueur et de largeur des pétales des fleurs) et les étiquettes de classe correspondantes lab. Le modèle est entraîné à trouver des relations entre les données d'entrée et les étiquettes de classe pour faire des prédictions sur de nouvelles données.
4. Copier le code

   prediction = model.predict([[longueur,largeur]])

   : Cette ligne permet d'effectuer une prédiction pour un couple [longueur, largeur] (dans l'exemple ci-dessus "longueur=2.5" et "largeur=0.75"). La variable "prediction" contient alors le label trouvé par l'algorithme knn. Attention, "prediction" est une liste Python qui contient un seul élément (le label), il est donc nécessaire d'écrire "predection[0]" afin d'obtenir le label.

Vous devriez normalement obtenir ceci :

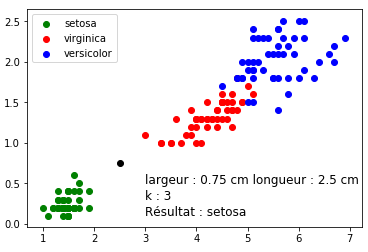
Entraînement 3 :

Modifiez le programme du "l'Entraînement 2" afin de tester l'algorithme knn avec un nombre "de plus proches voisins" différent (en gardant un iris ayant une longueur de pétale égale à 2,5 cm et une largeur de pétale égale à 0,75 cm). Que se passe-t-il pour k = 5 ?

Entraînement 4 :

Testez l'algorithme knn (toujours à l'aide du programme du "l'Entraînement 2") avec un iris de votre choix (si vous ne trouvez pas d'iris, vous pouvez toujours inventer des valeurs ;-))

Entraînement 5 :

Dans le quadrillage ci-dessous 14 points sont dessinés, dont 7 de la classe C1, avec des ronds noirs ∙, et 7 de la classe C2, avec des losanges ◊. On introduit un nouveau point A, dont on cherche la classe à l'aide d'un algorithme des k plus proches voisins pour la distance géométrique habituelle, en faisant varier la valeur de k parmi 1, 3 et 5.
Quelle est la bonne réponse (sous la forme d'un triplet de classes pour le triplet (1,3,5) des valeurs de k) ?

Voir une solution

Solution

Lorsque k = 1, le point le plus proche d'A est un losange, donc la classe prédite pour A est C2.
Lorsque k = 3, les trois points les plus proches d'A sont deux carrés et un losange, donc la classe prédite pour A est C1.
Lorsque k = 5, les cinq points les plus proches d'A comprennent trois carrés et deux losanges, donc la classe prédite pour A est C1.
Ainsi, la réponse est (C2, C1, C1) pour le triplet (1, 3, 5) des valeurs de k.

Masquer

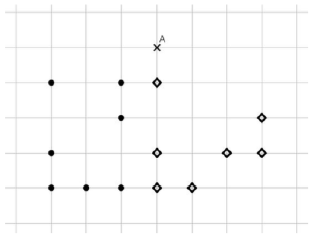
Entraînement 6 :

Arrivé dans la cantina de la planète Tatooine, Han Solo décide de donner des indications à Luke pour qu’il ne provoque pas les extraterrestres belliqueux. Il repère quelques caractéristiques et vous demande de l’aider à fournir des éléments à Luke pour ne pas créer de problèmes et donc pouvoir définir un extraterrestre belliqueux.

Couleur	Taille	Poids	Yeux par pair ?	Belliqueux
jaune	moyenne	léger	non	non
jaune	grande	moyen	oui	oui
vert	petite	moyen	oui	oui
jaune	petite	moyen	non	non
rouge	moyenne	lourd	non	non
vert	grande	lourd	non	oui
vert	moyenne	lourd	non	oui
jaune	petite	léger	oui	oui

De qui doit se méfier Luke ?
Élaborez les critères pour pouvoir mettre en œuvre KNN sur cet exemple.

Voir une solution

Solution

Luke doit se tenir à l'écart des extraterrestres verts et des extraterrestres jaunes avec les yeux par pair.

Masquer

Entraînement 7 : Exercice sur les baguettes magiques

Dans l'univers d'Harry Potter, les baguettes magiques sont des objets très importants pour les sorciers. Chaque baguette est unique et possède des caractéristiques qui la distinguent des autres baguettes.

Voici un tableau qui répertorie les caractéristiques de six baguettes magiques :

Baguette	Longueur (en pouces)	Flexibilité (en degrés)	Catégorie
B1	27	0	0
B2	33	1	0
B3	29	1	1
B4	30	0	0
B5	25	1	2
B6	31	0	0

Chaque baguette appartient à l'une des quatre catégories suivantes : sorbier (0), houx (1), if(2) ou vigne (3).

1. Utilisez l'algorithme des k-plus proches voisins (k-NN) avec k=3 pour déterminer les trois baguettes les plus proches de la baguette B7, qui possède les caractéristiques suivantes : longueur = 28 pouces, flexibilité = 1 degré, catégorie = 0. Voir une solution

   Solution

   Les trois baguettes les plus proches de B7 sont B1, B4 et B6. En effet, en utilisant l'algorithme des k-plus proches voisins avec k=3, on calcule les distances entre B7 et chaque baguette du tableau en utilisant la formule de distance euclidienne. Les distances sont les suivantes :

   • B1 : √((27-28)² + (0-1)² + (0-0)²) ≈ 1,41
   • B2 : √((33-28)² + (1-1)² + (0-0)²) ≈ 5,00
   • B3 : √((29-28)² + (1-1)² + (1-1)²) ≈ 1,00
   • B4 : √((30-28)² + (0-1)² + (0-0)²) ≈ 2,24
   • B5 : √((25-28)² + (1-1)² + (2-0)²) ≈ 3,61
   • B6 : √((31-28)² + (0-1)² + (0-0)²) ≈ 3,16

   Les trois baguettes les plus proches sont donc B1, B4 et B6, car ce sont celles qui ont les distances les plus courtes par rapport à B7.

   Masquer

2. Quelle est la catégorie de baguette la plus fréquente parmi les trois baguettes les plus proches de B7 ? Voir une solution

   Solution

   La catégorie de baguette la plus fréquente parmi les trois baguettes les plus proches de B7 est la catégorie sorbier, car deux des trois baguettes (B1 et B6) appartiennent à cette catégorie.

   Masquer

3. En déduisant la catégorie à laquelle appartient la baguette B7, pouvez-vous prédire la catégorie de cette baguette ? Voir une solution

   Solution

   En déduisant la catégorie à laquelle appartient la baguette B7, on peut prédire que cette baguette appartient à la catégorie sorbier, car les trois baguettes les plus proches de B7 sont toutes des baguettes sorbier.

   Masquer

Bonne chance !

Voir le code

Solution

Copier le code

import numpy as np

# Les données
X = np.array([[27, 0, 0], [33, 1, 0], [29, 1, 1], [30, 0, 0], [25, 1, 2], [31, 0, 0]])
y = np.array([0, 1, 2, 1, 3, 0]) # 0 = sorbier, 1 = houx, 2 = if, 3 = vigne

# La nouvelle baguette à classer
new_X = np.array([[28, 1, 0]])

# Calcul de la distance euclidienne entre la nouvelle baguette et toutes les autres baguettes
distances = np.sqrt(np.sum((X - new_X)**2, axis=1))

# Récupération des 3 indices des baguettes les plus proches
indices = np.argsort(distances)[:3]

# Comptage des catégories de baguettes
counts = np.bincount(y[indices])

# Catégorie la plus fréquente
most_frequent = np.argmax(counts)

# Affichage de la catégorie prédite pour la nouvelle baguette
if most_frequent == 0:
    print("La nouvelle baguette est une baguette en sorbier.")
elif most_frequent == 1:
    print("La nouvelle baguette est une baguette en houx.")
elif most_frequent == 2:
    print("La nouvelle baguette est une baguette en if.")
else:
    print("La nouvelle baguette est une baguette en vigne.")

Masquer