Tri par insertion et tri par sélection

Numérique et sciences informatiques

algorithme

Les algorithmes de tri des éléments d'un tableau ont une place à part en algorithmique. En effet, ils sont souvent utilisés pour mettre en évidence certains concepts algorithmiques (concepts que l'on retrouve dans d'autres types d'algorithmes).
Nous allons commencer par 2 algorithmes "classiques" : le tri par insertion et le tri par sélection.

Tri par sélection :

Le principe du tri par sélection/échange est d’aller chercher le plus petit élément de la liste pour l’échanger avec le premier, puis de repartir du second élément et d’aller chercher le plus petit élément de la liste pour l’échanger avec le second, etc...

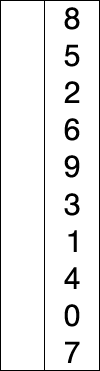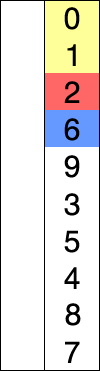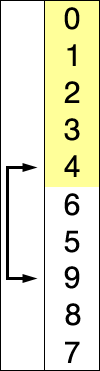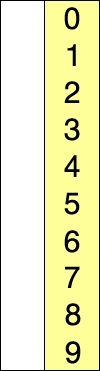
tri par selection
Tri par sélection
liste 8 5 2 6 9 3 1 4 0 7
On cherche le plus petit élément de la liste 8 5 2 6 9 3 1 4 0 7
On échange avec l’élément d’index 0. L’élément d’index 0 est « trié » 0 5 2 6 9 3 1 4 8 7
On cherche le plus petit élément dans la partie de la liste non triée 0 5 2 6 9 3 1 4 8 7
On échange avec l’élément d’index 1. La liste de l’index 0 à l’index 1 est « triée ». 0 1 2 6 9 3 5 4 8 7
On cherche le plus petit élément dans la partie de la liste non triée 0 1 2 6 9 3 5 4 8 7
La liste de l’index 0 à l’index 2 est « triée ». 0 1 2 6 9 3 5 4 8 7
On cherche le plus petit élément dans la partie de la liste non triée 0 1 2 6 9 3 5 4 8 7
On échange avec l’élément d’index 3. La liste de l’index 0 à l’index 3 est « triée ». 0 1 2 3 9 6 5 4 8 7
On cherche le plus petit élément dans la partie de la liste non triée 0 1 2 3 9 6 5 4 8 7
On échange avec l’élément d’index 4. La liste de l’index 0 à l’index 4 est « triée ». 0 1 2 3 4 6 5 9 8 7
ect 
procédure tri_selection(liste L)
   n ← taille de L
   pour i allant de 0 à n
      indice_du_min ← i
      pour j allant de i à n
         si L[j] < L[indice_du_min] alors
            indice_du_min ← j
      fin pour
      si indice_du_min ≠ i alors
         échanger L[i] et L[indice_du_min]
   fin pour
fin procédure

Entraînement 1 :

  1. Écrire une fonction tri_selection()en python
    2. def tri_selection(tableau):
    ...


# tests
assert tri_selection([1, 52, 6, -9, 12]) == [-9, 1, 6, 12, 52], "Exemple 1"
assert tri_selection([]) == [], "Exemple 2"
assert tri_selection([19]) == [19], "Exemple 3"
print("Tests  réussis")
  2. Déterminer un variant de la boucle for
    3. Solution

  3. Calculer la complexité de votre algorithme
    4. Solution

  4. Démontrer la terminaison de cet algorithme
    5. Solution


Fiche de cours

Tri par sélection :

Permutation des éléments
Principe :
  • Recherche du plus petit élément du tableau
  • Permutation avec la première case
  • Recommencer en partant de la seconde case
Comparaison = n²
Complexité = n²
def tri_selection(): ...

Tri par insertion :

Le tri par insertion est le tri que la majorité des joueurs de cartes occasionnels pratiquent intuitivement.
Il consiste à «traiter» toutes les cartes dans l’ordre découlant de la donne, le «traitement» se résumant, pour chaque carte, à l’insérer au bon endroit dans l’ensemble des cartes déjà triées.

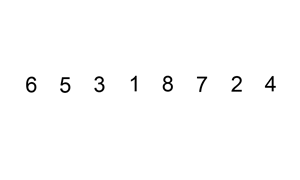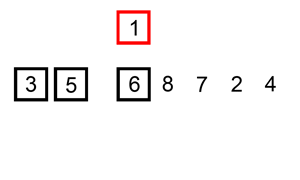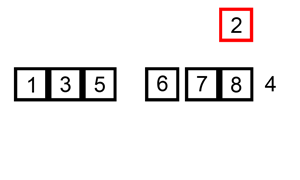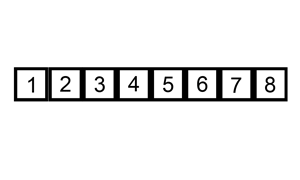
tri par insertion
Tri par insertion
liste 6 5 3 1 8 7 2 4
On décale les éléments de la liste triée de façon à insérer notre éléments : 6 5 3 1 8 7 2 4
La liste d’index 0 à 1 est triée, on va insérer l’élément d’index 2 dans cette liste : 5 6 3 1 8 7 2 4
On décale les éléments de la liste triée de façon à insérer notre éléments : 5 6 3 1 8 7 2 4
La liste d’index 0 à 2 est triée, on va insérer l’élément d’index 3 dans cette liste : 3 5 6 1 8 7 2 4
On décale les éléments de la liste triée de façon à insérer notre éléments : 3 5 6 1 8 7 2 4
La liste d’index 0 à 3 est triée, on va insérer l’élément d’index 4 dans cette liste : 1 3 5 6 8 7 2 4
La liste d’index 0 à 4 est triée, on va insérer l’élément d’index 5 dans cette liste : 1 3 5 6 8 7 2 4
On décale les éléments de la liste triée de façon à insérer notre éléments : 1 3 5 6 8 7 2 4
La liste d’index 0 à 5 est triée, on va insérer l’élément d’index 6 dans cette liste : 1 3 5 6 7 8 2 4
On décale les éléments de la liste triée de façon à insérer notre éléments : 1 3 5 6 7 8 2 4
La liste d’index 0 à 6 est triée, on va insérer l’élément d’index 7 dans cette liste : 1 2 3 5 6 7 8 4
On décale les éléments de la liste triée de façon à insérer notre éléments : 1 2 3 5 6 7 8 4
La liste est triée : 1 2 3 4 5 6 7 8 
procédure tri_insertion(liste L)
n ← taille de L
pour i allant de 1 à n # parcours du tableau
	temp ← L[i]
	j ← i
	tant que j > 0 et L[j-1] > temp faire
		L[j] ← L[j-1] # décalage
		j ← j - 1
	fin tant que
	L[j] ← temp # insertion au bon endroit
fin pour
fin procédure

Entraînement 2 :

  1. Écrire une fonction tri_insertion()en python en python
    2. def tri_insertion(tableau):
    ...


# tests
assert tri_insertion([1, 52, 6, -9, 12]) == [-9, 1, 6, 12, 52], "Exemple 1"
assert tri_insertion([]) == [], "Exemple 2"
assert tri_insertion([19]) == [19], "Exemple 3"
print("Tests  réussis")
  2. Déterminer un variant de la boucle while
  3. Démontrer la terminaison de cet algorithme
  4. Calculer la complexité de votre algorithme

Entraînement 3 :

Écrire un algorithme, en Python , qui vérifie qu’une liste est triée dans l’ordre croissant. L’algorithme doit renvoyer True si la liste est triée et False sinon.


Fiche de cours

Tri par insertion :

Permutation des éléments
Principe :
  • Parcourir le tableau à partir de la seconde case
  • Revenir en arrière et chercher la bonne position pour la valeur considérer
  • Décaler toutes les valeurs d'une case vers la droite
  • Placer la valeur
  • Recommencer en partant de la troisième case et ainsi de suite
Comparaison = n² / 2
Complexité = n²
def tri_insertion(): ...