Réseaux sociaux et graphes
Sciences numériques et technologie

Imaginez un réseau social ayant 6 abonnés (Alban, Béatrice, Cédric, Delphine, Eric et Fabienne) où :
- Alban est ami avec Béatrice, Cédric et Delphine
- Béatrice est ami avec Alban et Delphine
- Cédric est ami avec Alban, Eric et Delphine
- Delphine est ami avec tous les autres abonnés
- Eric est ami avec Cédric, Delphine et Fabienne
- Fabienne est ami avec Eric et Delphine
On peut représenter la situation précédente par un tableau à double entrée dans lequel il suffirait de faire une croix dans chaque case pour modéliser les relations d’amitié.
| ... | Alban | Béatrice | Cédric | Delphine | Eric | Fabienne |
|---|---|---|---|---|---|---|
| Alban | ... | .X. | .X. | .X. | ... | ... |
| Béatrice | .X. | ... | ... | .X. | ... | ... | Cédric | .X. | ... | ... | .X. | .X. | ... | Delphine | .X. | .X. | .X. | .X. | .X. | .X. | Eric | ... | ... | .X. | .X. | ... | .X. | Fabienne | ... | ... | ... | .X. | .X. | ... |
La description de ce réseau social, malgré son faible nombre d'abonnés, est déjà quelque peu rébarbative, alors imaginez cette même description avec un réseau social comportant des millions d'abonnés !
Il existe un moyen plus "visuel" pour représenter ce réseau social : on peut représenter chaque abonné par un cercle (avec le nom de l'abonné situé dans le cercle) et chaque relation "X est ami avec Y" par un segment de droite reliant X et Y ("X est ami avec Y" et "Y est ami avec X" étant représenté par le même segment de droite).
Voici ce que cela donne avec le réseau social décrit ci-dessus :
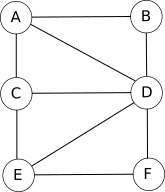
Ce genre de figure s'appelle un graphe. Les graphes sont des objets mathématiques très utilisés, notamment en informatique. Les cercles sont appelés des sommets et les segments de droites des arêtes.
Entraînement 1 :
Alban, Béatrice, Charles, Déborah, Éric, Fatima, Gérald, Hélène sont inscrits sur Facebook
-
Construisez le graphe de leur réseau social à partir des informations suivantes :
- Alban est ami avec Béatrice, Déborah, Eric et Fatima.
- Béatrice est amie avec Alban, Charles, Déborah et Eric.
- Charles, lui, est ami avec Béatrice et Déborah.
- Déborah est amie avec Charles, Béatrice et Alban.
- Eric, avec Béatrice et Alban.
- Fatima, avec Alban, Gérald et Hélène.
- Gérald, avec Fatima et Hélène.
- Hélène, avec Fatima et Gérald.
- Qui a le plus d’amis ? Le moins ?
- Un individu est-il isolé ? Peuvent-ils tous entrer en contact par le biais de leurs amis ?
Définitions sur les graphes :
Un graphe est un ensemble de sommets reliés par des arêtes.
La distance entre deux sommets d'un graphe est égale à la longueur du plus court chemin entre ces deux sommets,
Exemple : La distance entre le sommet A (graphe 1) et le sommet F est de 2 (chaîne A-D-F). ATTENTION : on parle bien du nombre minimum d'arêtes, A-D-E-F est aussi une chaîne entre A et F mais dans ce cas, nous avons 3 arêtes.
L’écartement d’un sommet est la distance maximale entre ce sommet et les autres sommets du graphe en prenant le chemin le plus court.
| Sommet | Alban | Béatrice | Cédric | Delphine | Eric | Fabienne |
|---|---|---|---|---|---|---|
| Écartement | 2 | 2 | 2 | 1 | 2 | 2 |
On appelle diamètre d'un graphe G, la distance maximale entre les deux sommets les plus éloignés du graphe G (écartement maximal).
Exemple : Dans le graphe 1 la distance maximale entre 2 sommets est de 2, nous pouvons donc dire que le diamètre du graphe est de 2.
Le centre d’un graphe est l’ensemble des sommets d’écartement minimal. Il peut y en avoir plusieurs et il(s) se situe(nt) à une distance des autres sommets du graphe égale au rayon.
Un influenceur sur un réseau social donné est une personne située au centre du graphe.
Exemple : Le centre du graphe 1 est le sommet Delphine (écartement minimal).
Le rayon d’un graphe est l’écartement d’un des sommets du centre du graphe.
Entraînement 2 :
Soit le graphe suivant :
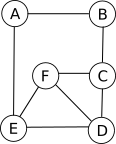
- Déterminer les écartements du graphe.
Sommet Alban Béatrice Cédric Delphine Eric Fabienne Écartement .?. .?. .?. .?. .?. .?. - Déterminez le (ou les) centre(s) du graphe 2
- En déduire le rayon du graphe 2.
- Déterminez le diamètre du graphe 2.
Entraînement 3 :
Soit le graphe suivant :
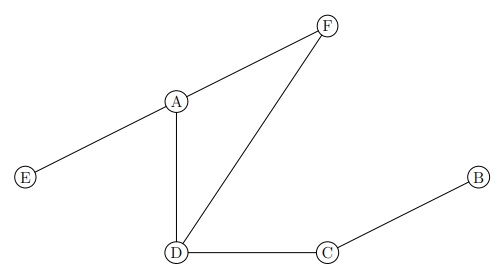
- Déterminer les écartements du graphe.
Sommet Alban Béatrice Cédric Delphine Eric Fabienne Écartement .?. .?. .?. .?. .?. .?. - Déterminez le (ou les) centre(s) du graphe 3
- En déduire le rayon du graphe 3.
- Déterminez le diamètre du graphe 3.
Le cyber Harcèlement
Pourquoi peut-on parler de harcèlement pour cet élève ?
On retrouve : la violence, la répétition, l'isolement.
Quand les attaques à répétition envers une personne passent derrière l’écran, on parle de cyber harcèlement. Une violence pourtant bien réelle. Si l’anonymat sur internet reste un droit, comment dénoncer et retrouver les harceleurs ? Comment se protéger ? Dans cet épisode : Léa fait un rêve affreux. Un garçon lui arrache ses vêtements en pleine rue et l’oblige à se montrer dans toute la ville. Quand elle raconte à sa copine Cindy, celle-ci lui répond que Léa a fait exactement la même chose mais en vrai, à son ex, Martin. Après s’être fait quitter, elle avait pratiqué le cyber-harcèlement sur lui.